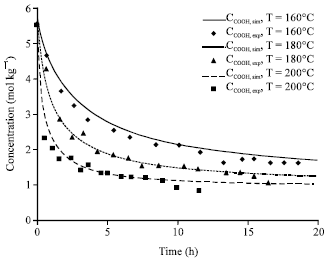
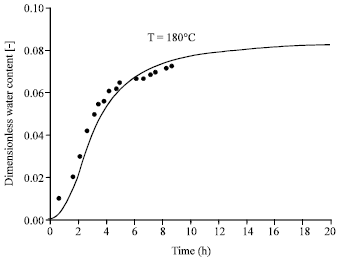
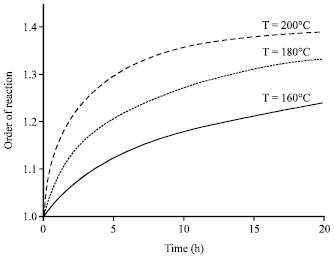
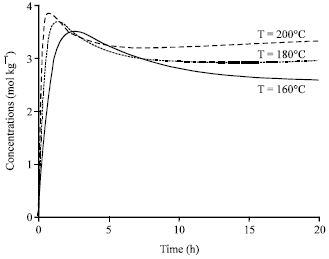
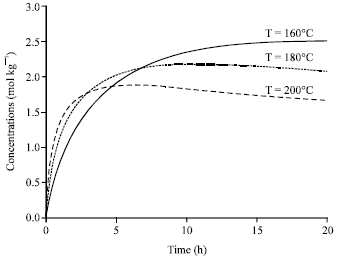
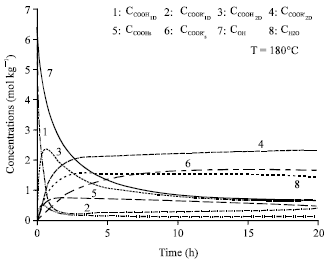
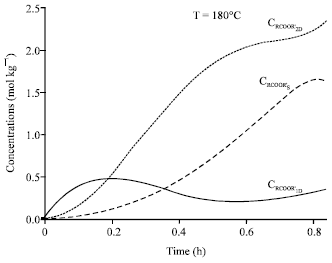
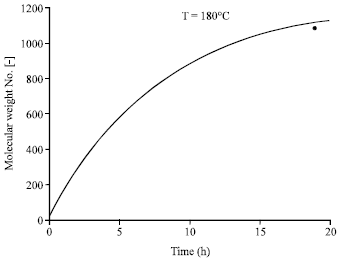
Research Article
Modelling and Simulation of an Unsaturated Polyester Process
Process Systems Engineering Group, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, 5600 MB, The Netherlands
E. Zondervan
Process Systems Engineering Group, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, 5600 MB, The Netherlands
A.B de Haan
Process Systems Engineering Group, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, 5600 MB, The Netherlands