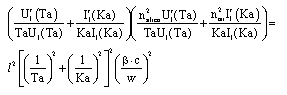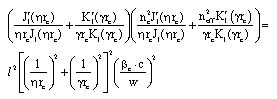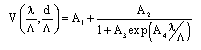Research Article
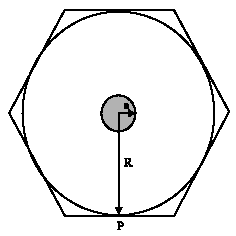
Comparison between Modified Fully Vectorial Effective Index Method and Empirical Relations Method for Study of Photonic Crystal Fibers
Islamic Azad University, Garmsar Branch, Islamic Republic of Iran
Mojtaba Mansourabadi
KN Toosi University of Technology Faculty of Electrical Engineering, Tehran, Islamic Republic of Iran
Hamed Baratvand
Department of Physics, Amirkabir University of Technology, Tehran, Islamic Republic of Iran