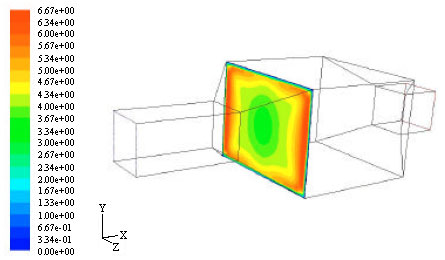
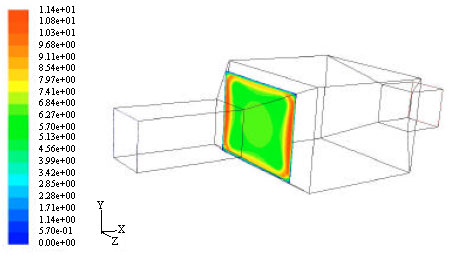
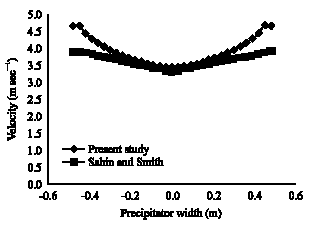
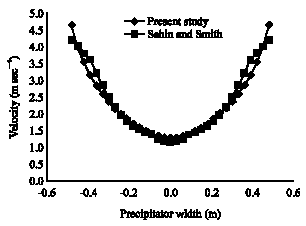
Research Article
Numerical Modelling of Flow through Perforated Plates Applied to Electrostatic Precipitator
Department of Mechanical Engineering, College of Engineering,Guindy Anna University Chennai, Chennai-600 025, Tamilnadu, India
N.V. Mahalakshmi
Department of Mechanical Engineering, College of Engineering,Guindy Anna University Chennai, Chennai-600 025, Tamilnadu, India