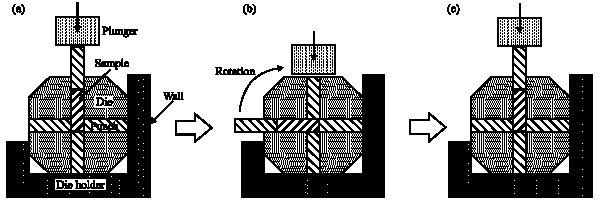
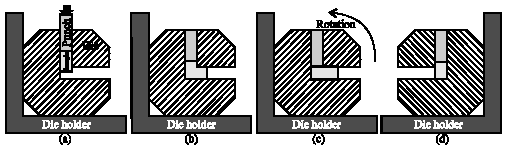
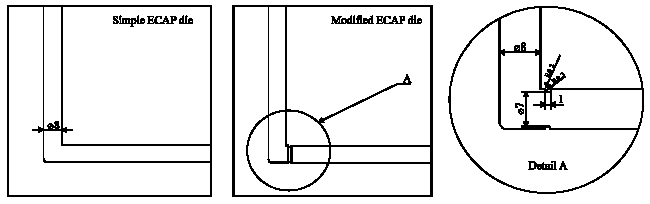
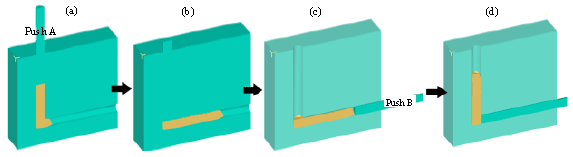
Research Article
Investigation of Strain Behavior in the Modified Equal Channel Angular Pressing Die by 3D Finite Element Method
Department of Mechanical Engineering, Iran University of Science and Technology, Tehran 16846-13114, Iran
Mahmood Ebrahimi
Department of Mechanical Engineering, Iran University of Science and Technology, Tehran 16846-13114, Iran