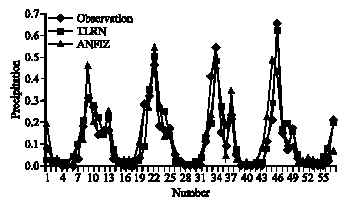
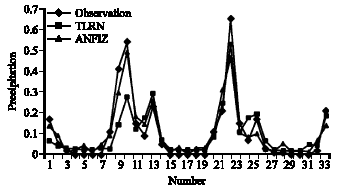
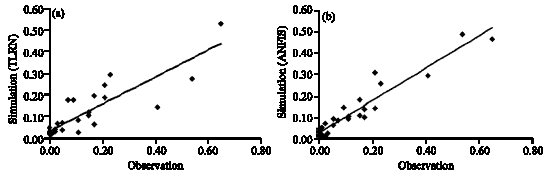
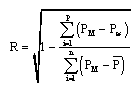Research Article
Application of ANN and ANFIS Models on Dryland Precipitation Prediction (Case Study: Yazd in Central Iran)
Faculty of Natural Resources, Yazd University, Iran
H. Afkhami
Faculty of Natural Resources, Yazd University, Iran
H. Sharifidarani
Faculty of Natural Resources, Yazd University, Iran
M. Dastorani
Department of Desert Land Management, Faculty of Natural Resources, Tehran University, Iran