Research Article
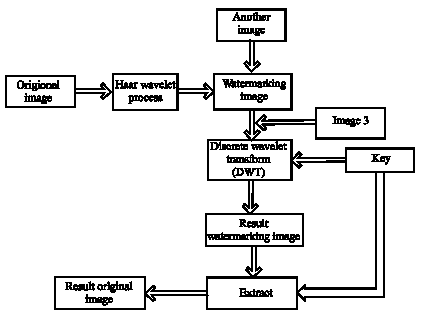
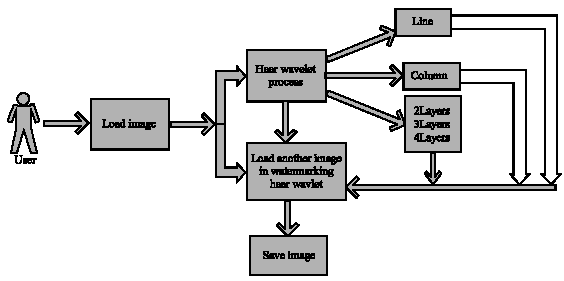
Digital Watermarking System based on Cascading Haar Wavelet Transform and Discrete Wavelet Transform
Faculty of Information Technology, Middle East University, P.O. Box 42, Postal Code 11610, Amman, Jordan
Adham Alshamary
Faculty of Information Technology, Middle East University, P.O. Box 42, Postal Code 11610, Amman, Jordan









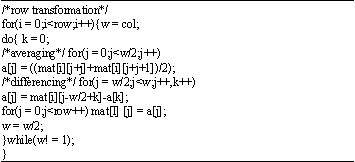
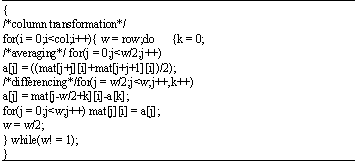




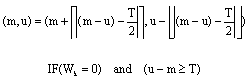
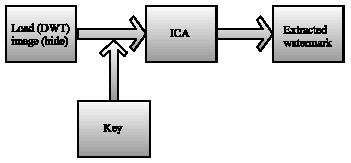


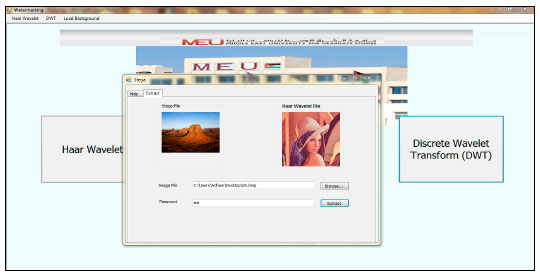
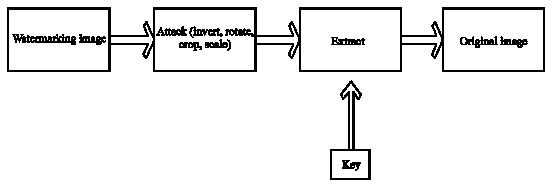
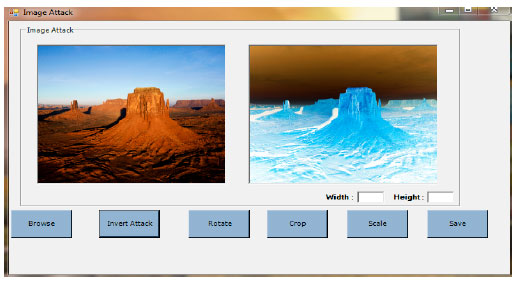
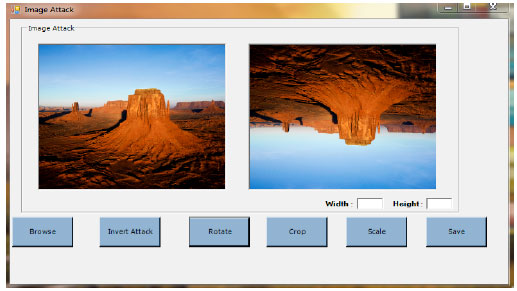











siti hajar binti ab aziz Reply
hi...i am hajar, and i am a Msc student from malaysia.
i am interested regarding your thesis..
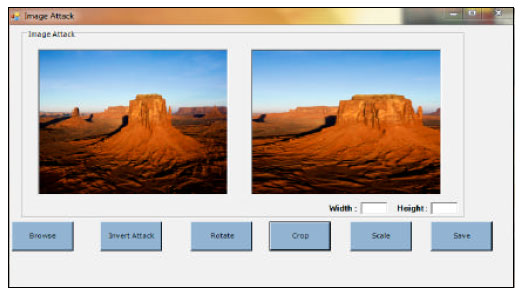
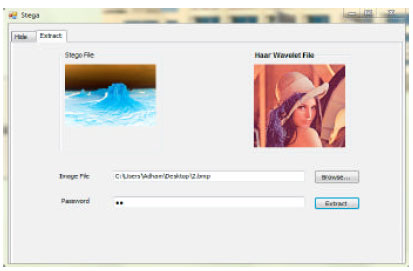
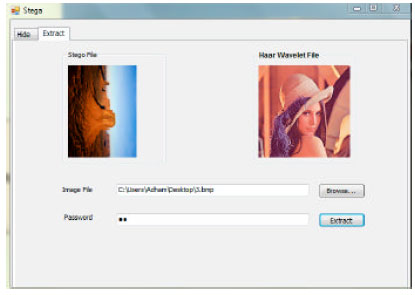
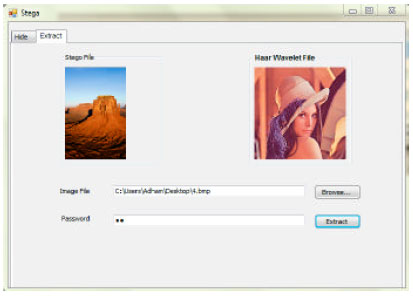
now i am doing my thesis regarding image watermarking, and its actually same like yours.except my scope is just dwt only.
hope you can share with me more about your coding..
regards..