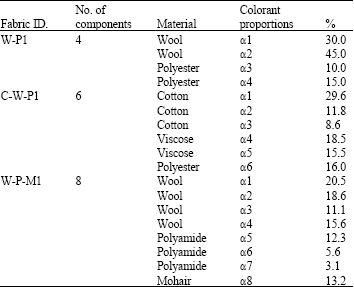
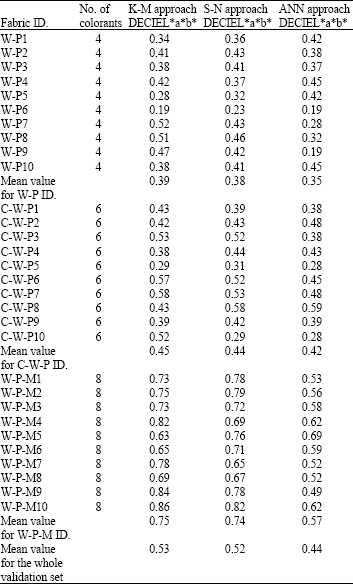
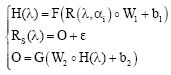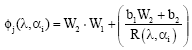Research Article
An As-Short-as-Possible Mathematical Assessment of Spectrophotometric Color Matching
Dipartimento di Meccanica e Tecnologie Industriali, Universit� degli Studi di Firenze, Via di Santa Marta 3, 50139, Firenze, Italy
M. Carfagni
Dipartimento di Meccanica e Tecnologie Industriali, Universit� degli Studi di Firenze, Via di Santa Marta 3, 50139, Firenze, Italy