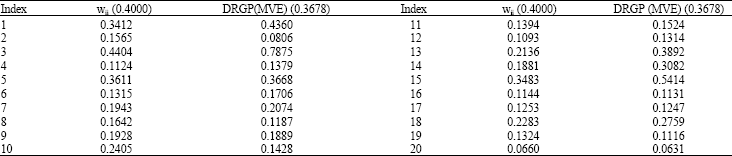
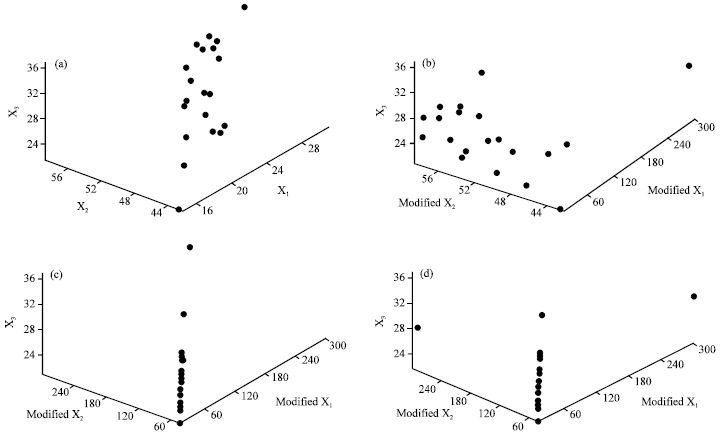
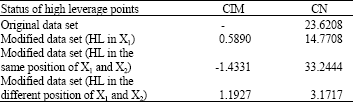
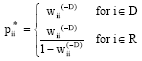Research Article
The Effect of Collinearity-influential Observations on Collinear Data Set: A Monte Carlo Simulation Study
Laboratory of Applied and Computational Statistics, Institute for Mathematical Research, University Putra Malaysia, 43400 Serdang, Selangor, Malaysia
Habshah Midi
Laboratory of Applied and Computational Statistics, Institute for Mathematical Research, University Putra Malaysia, 43400 Serdang, Selangor, Malaysia
A.H.M.R. Imon
Department of Mathematical Sciences, Ball State University, Muncie, IN 47306, USA