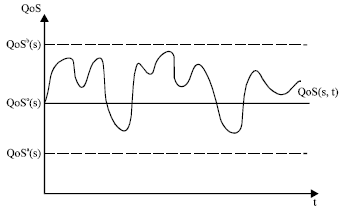
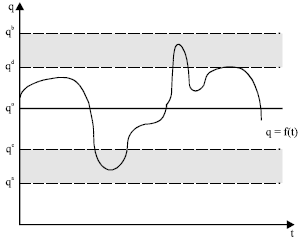
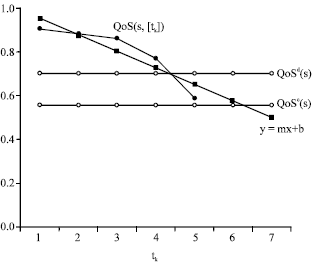
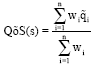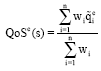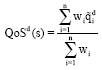Research Article
Continuous Monitoring System for Estimation the Quality of Service of Computer Network
Department of Information and Control System, Faculty of Computer Science, Kharkov National University of Radio Electronics, Ukraine
Mohammad Al Rawajbeh
Department of Management Information System, Faculty of Administrative and Financial Sciences, Al Isra Private University, Jordan
Alexandr Golubev
Department of Information and Control System, Faculty of Computer Science, Kharkov National University of Radio Electronics, Ukraine