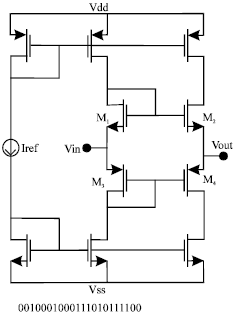
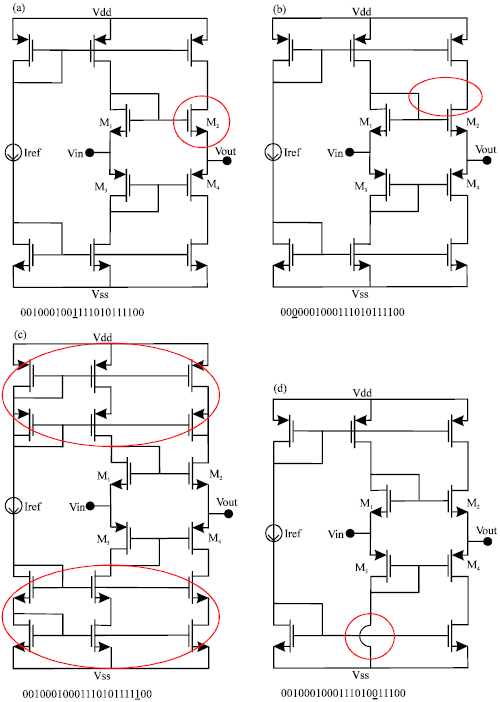
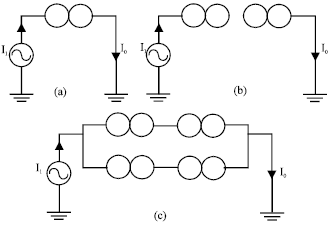
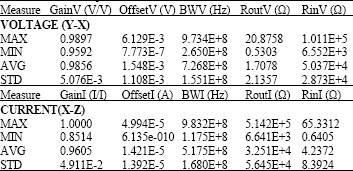
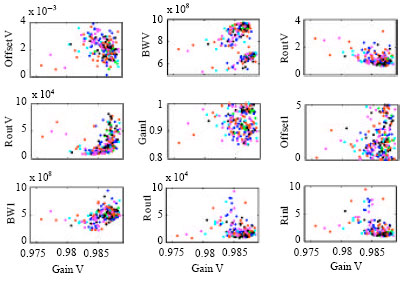
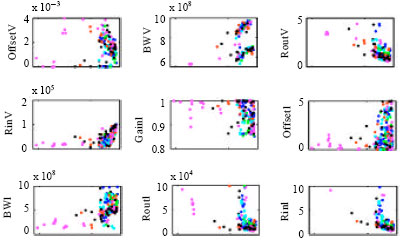
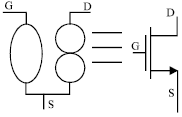Research Article
Applications of Evolutionary Algorithms in the Design Automation of Analog Integrated Circuits
INAOE. Luis Enrique Erro No. 1, Tonantzintla, 72840 Mexico
I. Guerra-Gomez
INAOE. Luis Enrique Erro No. 1, Tonantzintla, 72840 Mexico
M.A. Duarte-Villasenor
INAOE. Luis Enrique Erro No. 1, Tonantzintla, 72840 Mexico
Luis G. de la Fraga
CINVESTAV. Computer Science Department, Av. IPN 2508. 07360, Mexico
G. Flores-Becerra
Instituto Tecnol�gico de Puebla. Av. Tecnol�gico 420, 72220, Mexico
G. Reyes-Salgado
Department of Computer Sciences, Cuernavaca, 62490, Mexico
C.A. Reyes-Garcia
INAOE. Luis Enrique Erro No. 1, Tonantzintla, 72840 Mexico
G. Rodriguez-Gomez
INAOE. Luis Enrique Erro No. 1, Tonantzintla, 72840 Mexico