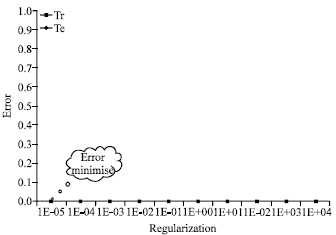
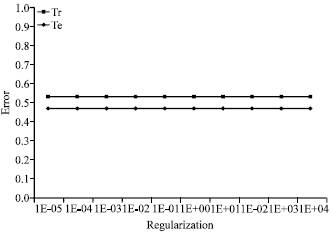
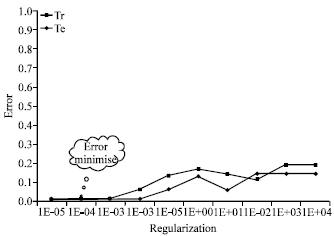
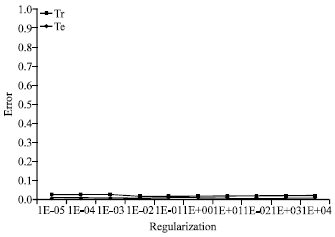
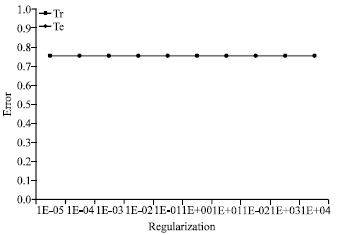
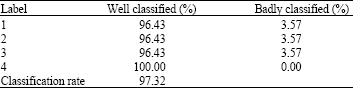
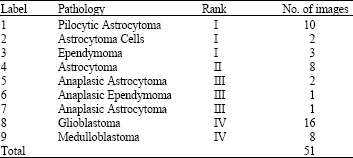
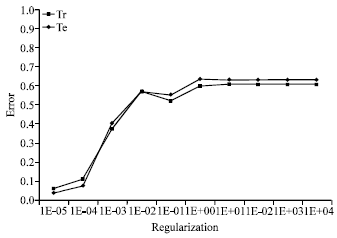
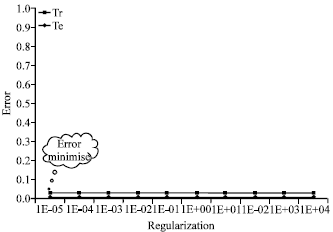
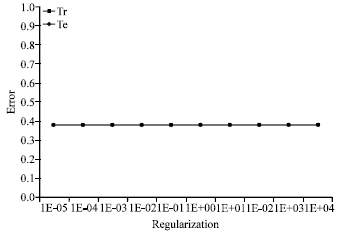
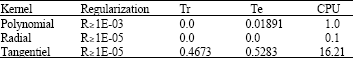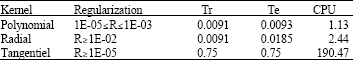Research Article
Support Vector Machines for Brain Tumours Cells Classification
Modeling and Optimization of Industrial Systems Laboratory, Department of Computer Science, Faculty of Science, University of Science and Technology of Oran, P.O. Box 1505, El Menaour, Oran, Algeria
M. Benyettou
Department of Computer Science, Faculty of Science and Technology, University of Mostaganem, B.P. 188, Mostaganem, Algeria