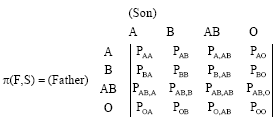
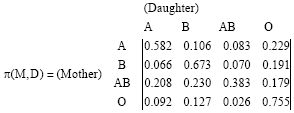
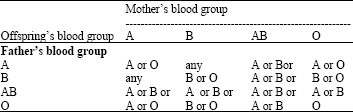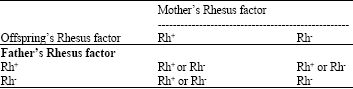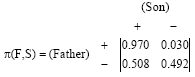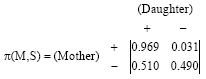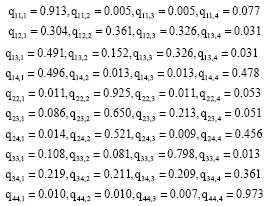Research Article
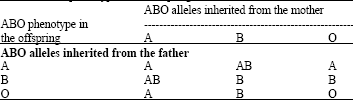
Linear and Nonlinear Models of Heredity for Blood Groups and Rhesus Factor
Institute of Mathematics and Information Technology, 100125, Tashkent, Uzbekistan
J.I. Daoud
Faculty of Engineering, IIUM, 50728, Kuala Lumpur, Malaysia
M. Usmanova
Faculty of Science, IIUM, 25200, Kuantan, Malaysia