Research Article
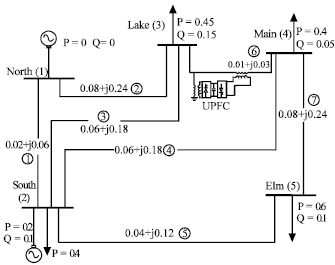
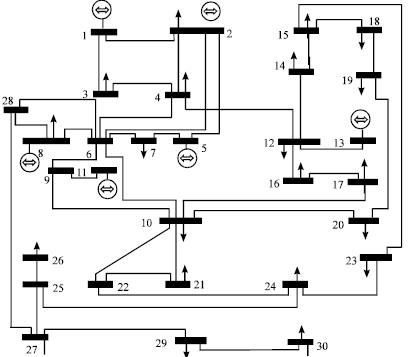
Power Flow Study Including FACTS Devices
Department of Electrical and Electronics Engineering,SSN College of Engineering, OMR, Kalavakkam, TN-603 110, India
S.S. Dash
Department of Electrical and Electronics Engineering,SRM University, Katankulathur, Tamil Nadu, 603 203, India
T. Thyagarajan
Department of Instrumentation Engineering, MIT, Anna University, Chennai, India









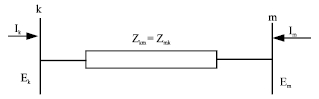
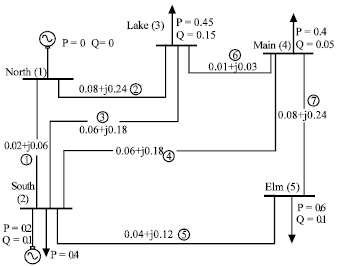
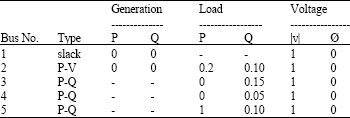
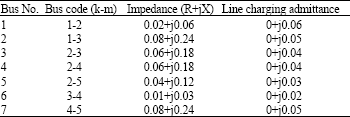
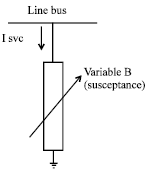
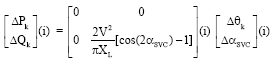
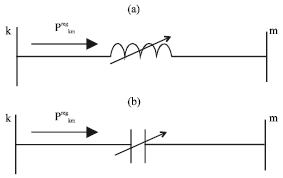
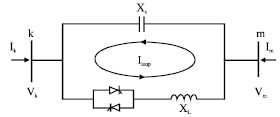


Shilpashree Reply
Will you please send this article to my mail as I am not able to download the pictures in this paper