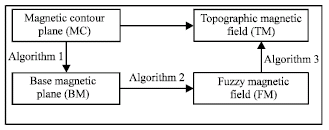
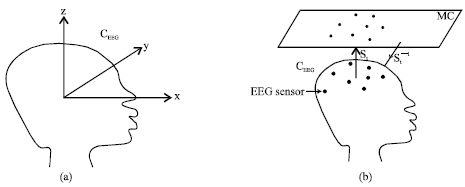
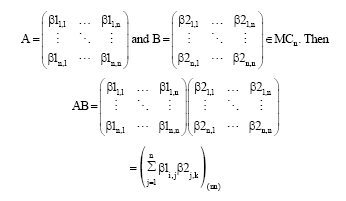
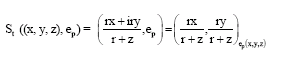Research Article
Semigroup of EEG Signals during Epileptic Seizure
Theoretical and Computational Modeling for Complex Systems, Department of Mathematics,Ibnu Sina Institute for Fundamental Science Studies, Universiti Teknology Malaysia,81310 Skudai, Johor, Malaysia
T. Ahmad
Theoretical and Computational Modeling for Complex Systems, Department of Mathematics,Ibnu Sina Institute for Fundamental Science Studies, Universiti Teknology Malaysia,81310 Skudai, Johor, Malaysia