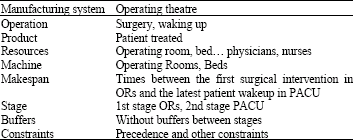
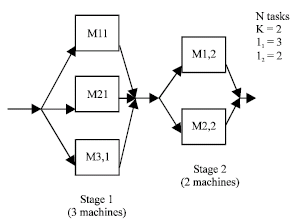
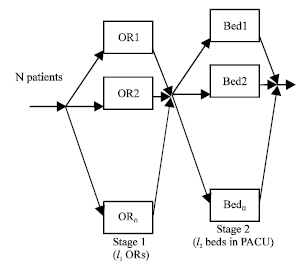
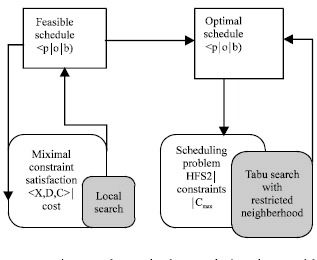
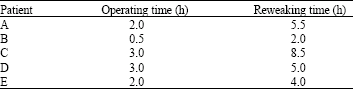
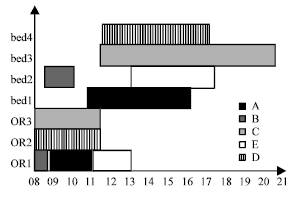
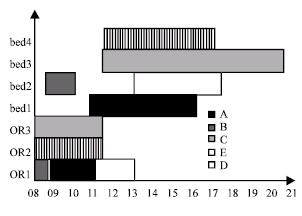
Research Article
Operating Theatre Scheduling Under Constraints
LAMOSI Laboratory, Department of Computer Science, Faculty of Sciences,University of Sciences and Technology, Oran USTO, BP. 1505 Oran M�Naouer 31000, Algeria
K. Belkadi
LAMOSI Laboratory, Department of Computer Science, Faculty of Sciences,University of Sciences and Technology, Oran USTO, BP. 1505 Oran M�Naouer 31000, Algeria