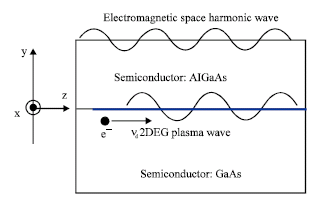
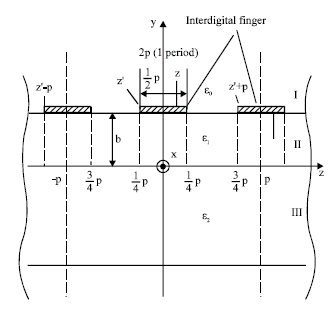
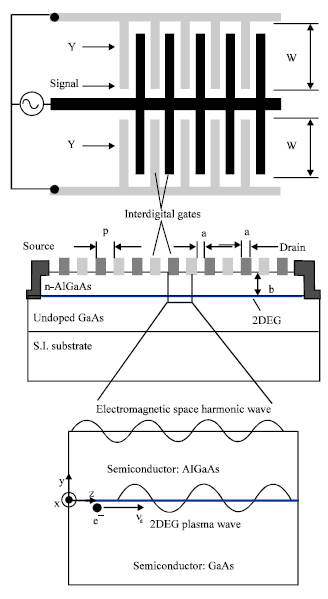
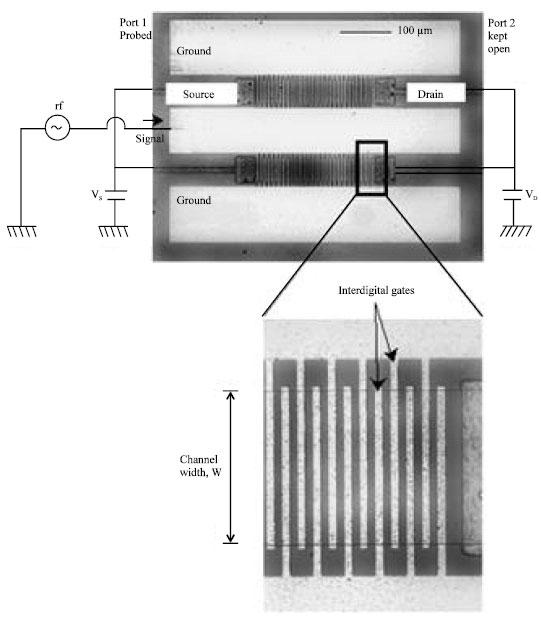
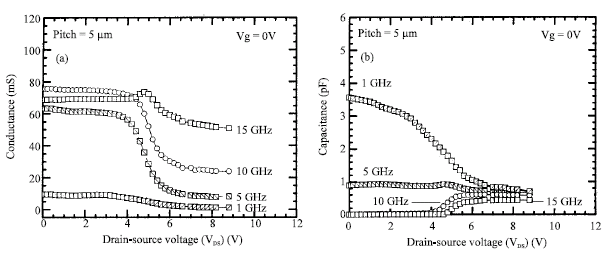
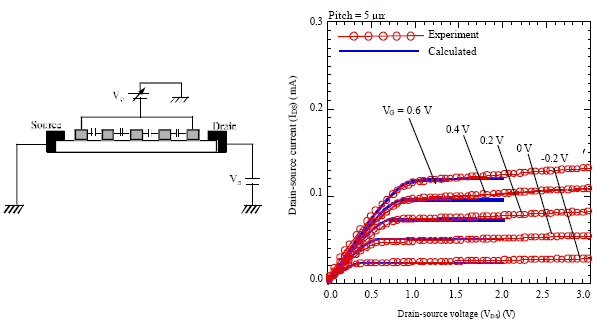
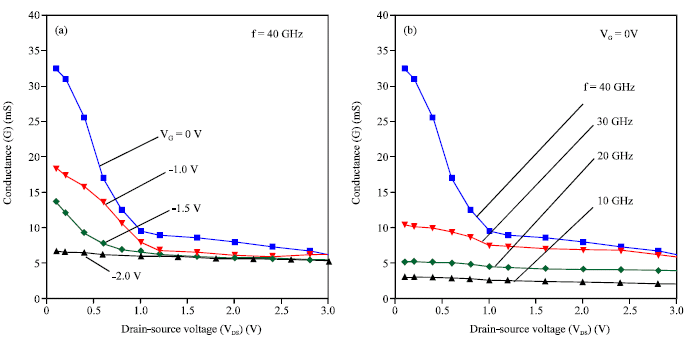
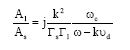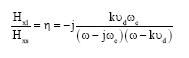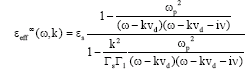Review Article
Plasma Wave Electronics: A Revival Towards Solid-State Terahertz Electron Devices
Material Innovations and Nanoelectronics Research Group, Faculty of Electrical Engineering, Universiti Teknologi Malaysia, 81310 UTM Skudai, Johor, Malaysia
A.M. Hashim
Material Innovations and Nanoelectronics Research Group, Faculty of Electrical Engineering, Universiti Teknologi Malaysia, 81310 UTM Skudai, Johor, Malaysia