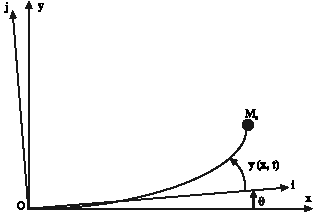
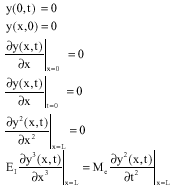
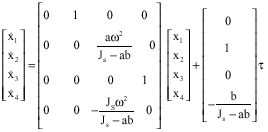
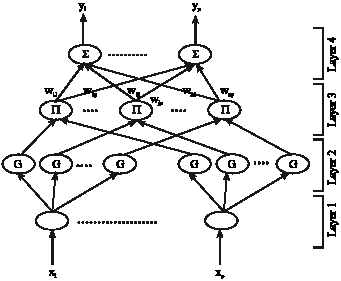
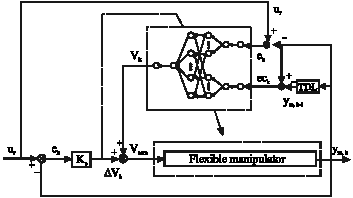
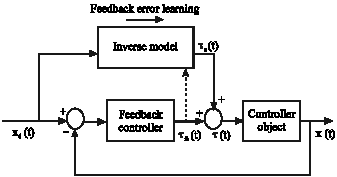
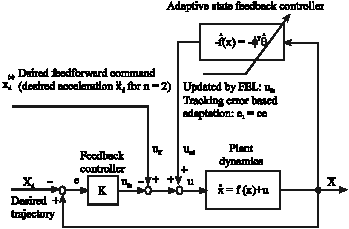
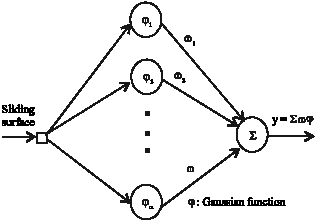
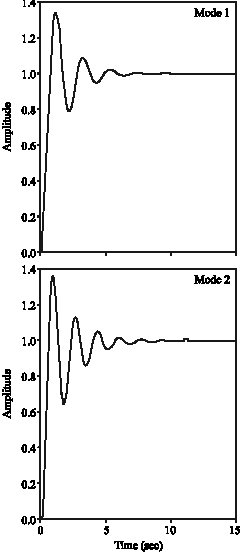
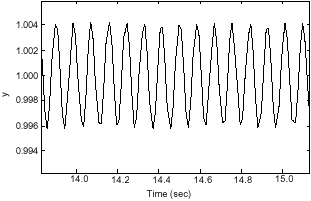
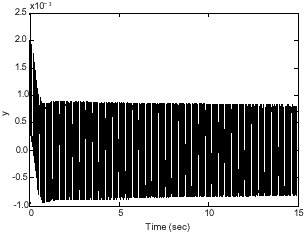
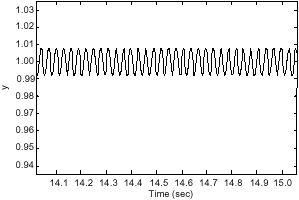
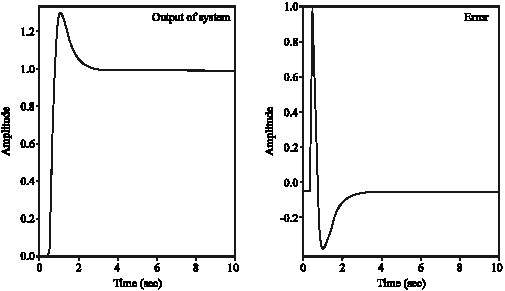
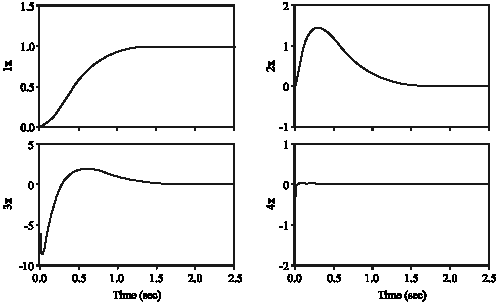
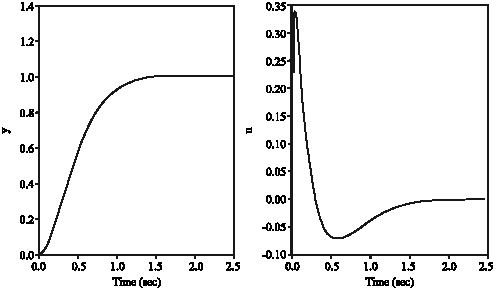
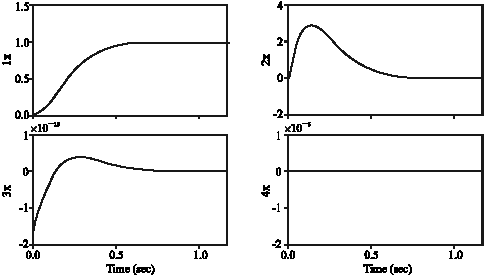
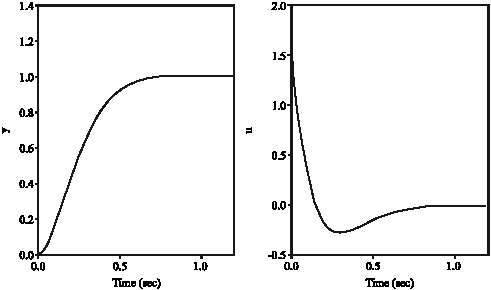
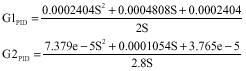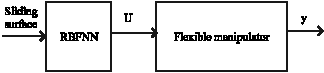Research Article
Hybrid Control of Flexible Manipulator
Department of Mechatronics Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran
M. Aliyari Shoorehdeli
Department of Electrical Engineering, K.N.T University of Technology, Tehran, Iran
M. Teshnehlab
Department of Electrical Engineering, K.N.T University of Technology, Tehran, Iran
M.A. Nekoui
Department of Electrical Engineering, K.N.T University of Technology, Tehran, Iran