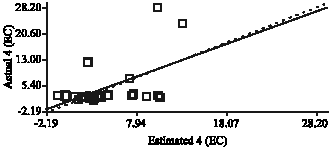
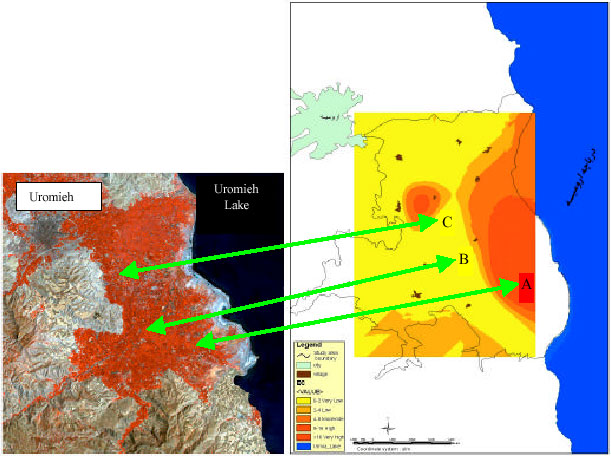
Research Article
Comparative Efficacy of Some Geostatistical Methods for the Estimation of Spatial Variability of Topsoil Salinity
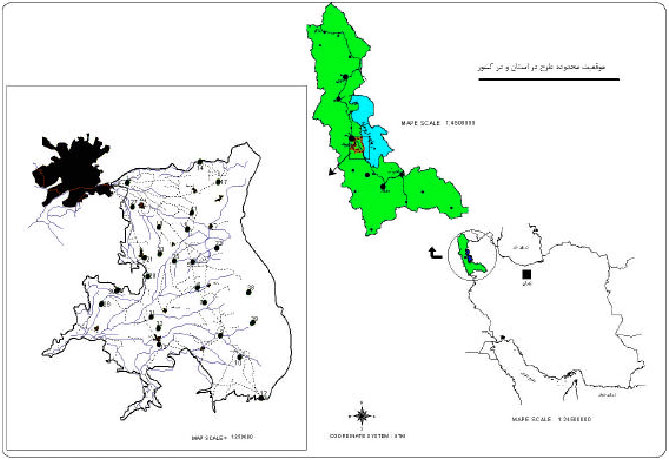
Research Center of Agricultural and Natural Resources of West Azarbaijan, P.O. Box 365, Uromieh, Islamic Republic of Iran
M.H. Mahdian
Soil Conservation and Watershed Management Institute, Iran