ABSTRACT
In this study, change of moisture distribution in wood is analyzed by finite element technique. Diffusion of moisture during drying and conduction of heat can be defined by Fourier law. Due to this similarity, heat conduction module is used to estimate the moisture diffusion. Ansys version 12 is used in modeling. Network is created with 2 dimensional link 32 elements. For modeling, the wood types which we know their moisture diffusion coefficients from earlier studies are selected. The properties of a panel having the dimension of 50x1000x1000 mm are used. Moisture diffusion coefficient under fiber saturation point is assumed as constant. Air-drying of wood plates having 40% moisture content in an environment having 10% moisture content is modeled.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2009.4091.4094
URL: https://scialert.net/abstract/?doi=jas.2009.4091.4094
INTRODUCTION
New technologies make the new materials available for use but wood keeps its importance. Wood is a light but strength material. It can be machined and coated easily. It has a high resistance to noise and heat transfer but, moisture is a disadvantage for wood. Moisture ratio in wood affects its mechanical and thermal properties so, it is dried before use. Drying process aims to decrease the moisture ratio without destroying the cell structure of wood. It is a costly process but highly increases the value of wood (Bozkurt and Göker, 1996).
There are different techniques of drying (Kantay, 1993). In technical drying heat, moisture and pressure are controlled. There may be some air circulation also. Natural drying technique is widely used because of its low cost. In natural drying, temperature of drying environment, moisture ratio, direction and velocity of circulating air are very important.
Drying of wood without any deformation at the possible shortest time is very important. So, the estimation of drying time is important for cost analysis and planning of manufacture.
There are many mathematical models for drying but, due to the impossibility of inclusion of all of the factors, the estimation of real time is impossible. The density of wood, the thickness and other dimensions of dried plate, moisture ratio and distribution of moisture, the moisture gradient between the wood and the environment, fiber structure of wood, environmental temperature, chemical properties of liquid extracted from the wood, the temperature, direction and velocity of the drying air are the main factors (Siau, 1983). In the developed models, the moisture ratio along the thickness is assumed as constant. In practice, to make the moisture ratio same along the thickness, normalization process is preferred. The parameters in mathematical models are variable so, they are defined as semi practical. As the practical techniques needs some time and mathematical models are insufficient, finite element techniques may be used. So, we studied on the finite element analysis by software of drying in an environment having no air circulation.
Babiak (1998) measured the coefficient of moisture diffusion of beech and black locust in radial, longitudinal and radial direction for 20 and 60°C. It was high in 60°C than in 20°C. Resch et al. (1989) developed a computer software program for drying of Dougles fir lumber. Simpson (1993) experimentally determined the diffusion coefficients of northern red oak. Simpson and Hart (2001) developed a computer software program for estimating the air-drying times of some woods. Fotsing and Tchagang (2005) experimentally determined the diffusion coefficients of wood in isothermal conditions. Khazai (2007), studied the water absorption characteristics of woods and calculated the diffusion coefficients for Acer sp., Ojamlesh and pinus sp. wood.
MATERIALS AND METHODS
This study was conducted in Middle East Technical University Technology Incubation Center on 2009.
Coefficients of moisture diffusion picked up from different studies are given in Table 1 (Babiak, 1998; Simpson, 1993; Simpson and Hart, 2001). In Table 1 the temperature of the environment for coefficient of moisture diffusion for different wood types is given, because the diffusion rate increases exponentially with temperature (Simpson and Hart, 2001).
| Table 1: | Diffusion coefficient of moisture of some woods |
 | |
As shown in the Table 1, ponderosa pine has the highest coefficient of moisture diffusion and Douglas fir has the lowest. Those values are used in the finite element analysis which will be explained. Ansys version 12 of finite element analysis software is used to solve the problem of moisture distribution in wood during drying (Ansys, 2009). Heat analysis problems module of this software solves the following Fourier equation (Incropera and de Witt, 1990).
Where:
| cp | = | Heat capacitance |
| k | = | Heat conduction coefficient |
| t | = | Time |
| T | = | Temperature |
| x, y, z | = | Coordinates |
| ρ | = | Density |
| q. | = | Heat produced |
If we assume that the coefficient of heat transfer in x, y and z direction is constant and there is no energy production, Fourier equation is simplified and becomes:
 |
Due to the similarity between heat conduction and moisture distribution, if D is assumed as constant and there is no production of moisture; one dimensional moisture distribution problem may also be defined by Fourier equation. D means the rate of diffusion of water from internal sections to outside surface.
Thickness of wood is assumed as 50 mm with 1 m2 surface area.
 | |
| Fig. 1: | Thickness of wood |
Moisture movement above the fiber saturation point is a combination of diffusion and mass flow driven by a partial gradient. For that reason, the diffusion analysis can be used when wood has first pre-dried to below the fiber saturation point. So, moisture content (Ni) at the beginning of drying process was chosen as 40% and the final moisture content (Nd) is assumed to be the same with external environment which is 10%.
In reality, the diffusion coefficient of moisture in wood is different in longitudinal, radial and tangential directions. That ratio is reported as different in some studies (Liu and Simpson, 1997). In a study, diffusion coefficient of moisture in radial direction is 15-20% higher than tangential direction and 2.2 - 2.7 times in longitudinal direction (Fotsing and Tchagang, 2005). In our study, we assumed that diffusion coefficient of moisture is the same in all directions and resistance of wood to moisture diffusion is assumed as negligible. As the initial and final moisture ratios are assumed as 40 and 10%, respectively, Nmean is calculated as 30% by the following formula (Siau, 1983):
Thickness of the panel is very low as compared with other dimension, so it is modeled as one dimensional. The geometry of the panel was symmetric so, modeling half of the thickness is assumed to be sufficient as shown in Fig. 1. In network, 10 link 32 elements (E1 to E10) at equal distances are used as shown in Fig. 2.
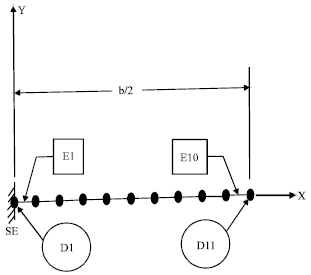 | |
| Fig. 2: | Element E points on thickness |
RESULTS AND DISCUSSION
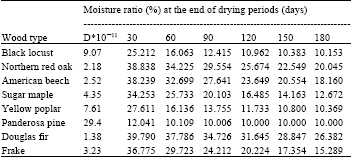
The moisture ratio at the center of the thickness of wood panels after 30, 60, 90,120, 150 and 180 days for eight different types of wood are obtained from the Ansysy software v.12 by entering the coefficient of moisture diffusion and given in Table 2. Iteration time in the estimation of drying times is selected as six days. The highest decrease in moisture content at the end of 180 days is in ponderosa pine (10.000%) followed by black locust (10.153%), yellow poplar (10.369%) and sugar maple (12.672%). The lowest decrease in moisture content is in Douglas fir (26.382%) followed by Northern red oak (20.045%), American beech (18.160%) and frake (15.289%) at the end of 180 days. Those results are compatible with the values given by Kantay (1993).
As shown in Fig. 3, moisture ratio decreases by time but the amount of decrease is not the same for all types of woods. At the early days of drying process, the liquids move from the inside of the wood to the surface but, later on this flow rate decreases.
By using the same software, it is also possible to determine the moisture distribution along the thickness of wood panels at the end of different periods or the time necessary to reach to an expected moisture ratio i.e., x days to reach from 35% moisture ratio to 15% in yellow poplar having a thickness of 100 mm.
It was reported that as the moisture ratio decreases, the moisture diffusion rate also decreases (Simpson, 1993). In Northern red oak, as the moisture ratio decreases from 30 to 5%, the coefficient of moisture diffusion decreases exponentially up 30% and the drying process slows down (Simpson, 1993). Simpson (1993) notes 0.5% difference between the experimental found values and method of diffusion analysis in Northern red oak wood.
| Table 2: | Moisture diffusion coefficients and moisture ratios at the center of panels |
 | |
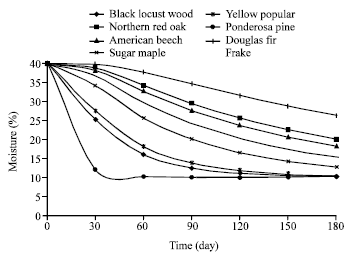 | |
| Fig. 3: | Moisture ratio change in some woods by time |
Rosen (1978) found that the effect of air velocity on drying time decreases rapidly above 3 m sec-1.
The result of this experiment supports the previous studies shown in the references.
CONCLUSION
The estimation of air-drying times of eight different types of woods with Ansys finite element analysis software is compatible with the experimentally founded values. So, Ansys finite element analysis software heat conduction module can be used for the estimation of drying times of wood in drying schedule planning. This analysis can be repeated successfully for other types of woods if the coefficient of moisture diffusion is known. This software is expected to increase the quality of drying planning of woods.
REFERENCES
- Fotsing, J.A.M. and C.W. Tchagang, 2005. Experimental determination of the diffusion coefficients of wood in isothermal conditions. J. Heat Mass Transfer, 41: 977-980.
CrossRef - Liu, J.Y. and W.T. Simpson, 1997. Solutions of diffusion equation with constant diffusion and surface emission coefficients. J. Drying Technol., 15: 2459-2477.
Direct Link - Resch, H., H. Kang and M. Hoag, 1989. Drying douglas fir lumber a computer simulation. Wood Fiber Sci., 21: 207-218.
Direct Link - Simpson, W.T., 1993. Determination and use of moisture diffusion coefficient to characterize drying of northern red oak. J. Wood Sci. Technol., 27: 409-420.
CrossRef - Simpson, W.T. and C.A. Hart, 2001. Method for estimating air-drying times of lumber. Forest Prod. J., 51: 51-63.
Direct Link








