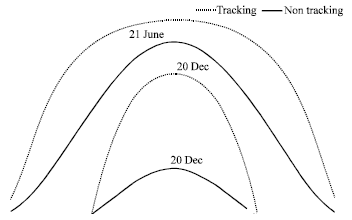
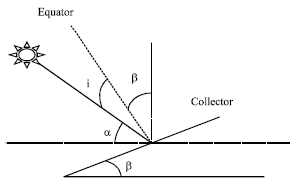
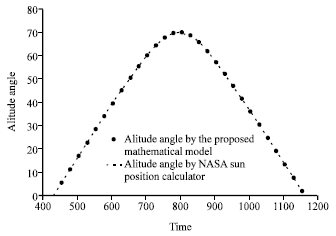
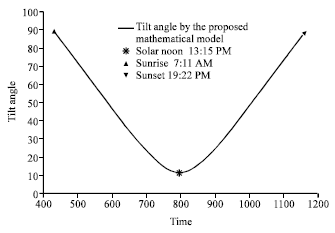
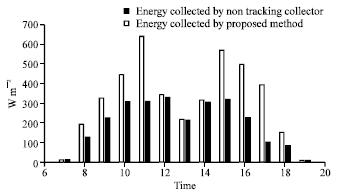
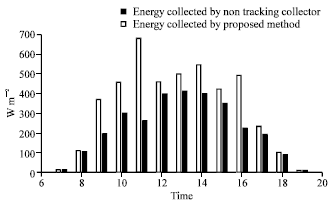
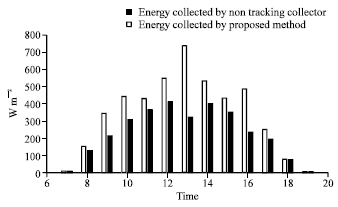
Research Article
A Novel Active Sun Tracking Controller for Photovoltaic Panels
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment, University Kebangsaan Malaysia, Bangi 43600, Selangor, Malaysia
A. Mohamed
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment, University Kebangsaan Malaysia, Bangi 43600, Selangor, Malaysia
R.J. Khan
Rachna College of Engineering and Technology, Gujranwala, Pakistan
N. Amin
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment, University Kebangsaan Malaysia, Bangi 43600, Selangor, Malaysia