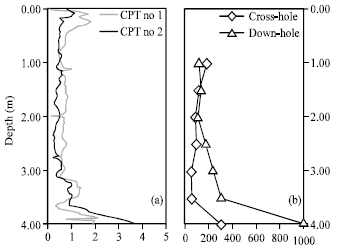
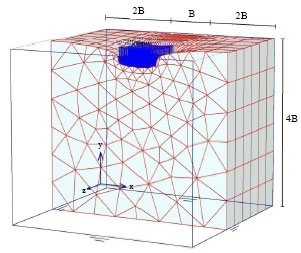
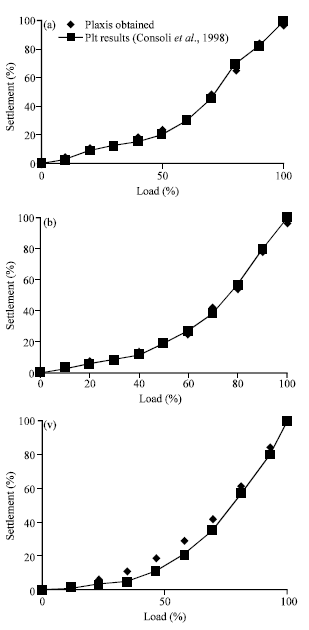
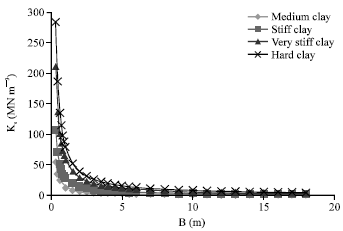
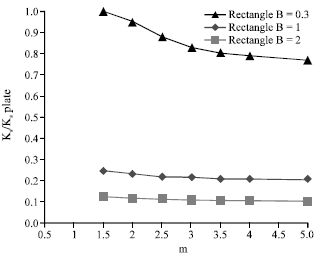
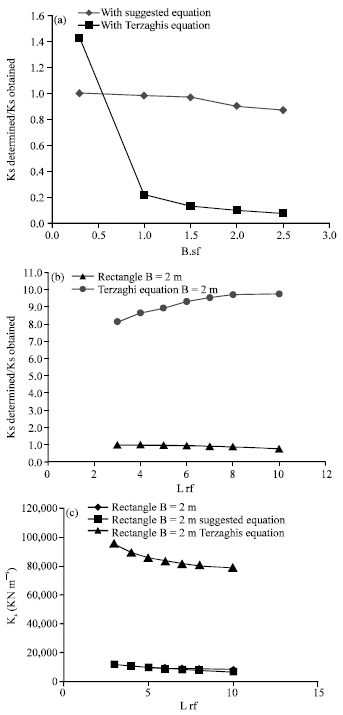
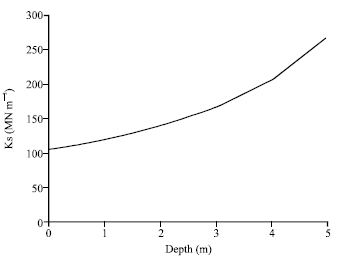
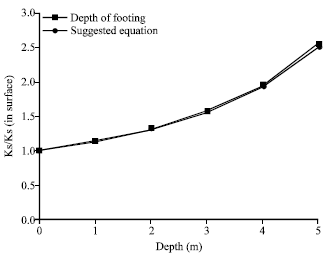
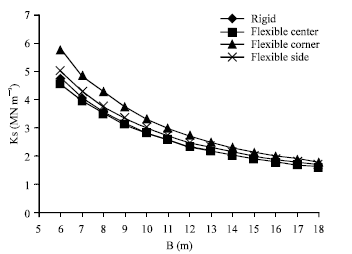
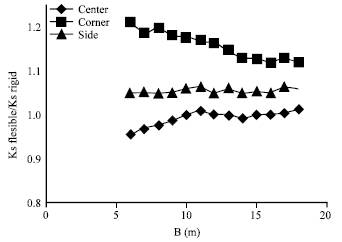
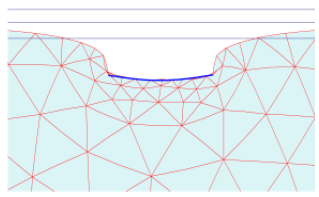
Research Article
Effective Parameters on Modulus of Subgrade Reaction in Clayey Soils
Department of Civil Engineering, Imam Khomeini International University, Qazvin, Iran
M. Janbaz
Imam Khomeini International University, Qazvin, P.O. Box 1469818144, Tehran, Iran