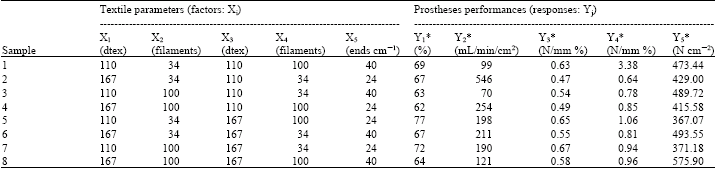
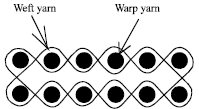
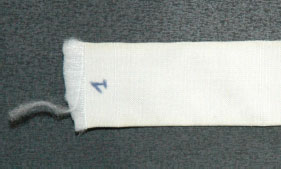
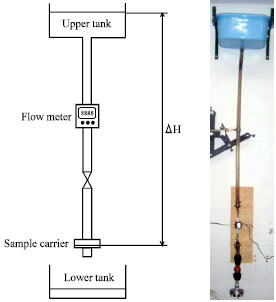
Research Article
Simultaneous Optimization of Plain Woven Vascular Prostheses Performances
Textile Research Unit, ISET of Ksar Hellal, 5070 Ksar Hellal, Tunisia
S. Ben Abdessalem
Textile Research Unit, ISET of Ksar Hellal, 5070 Ksar Hellal, Tunisia
F. Sakli
Textile Research Unit, ISET of Ksar Hellal, 5070 Ksar Hellal, Tunisia