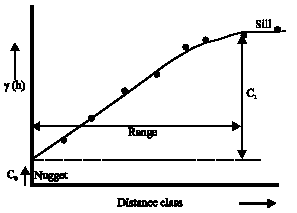
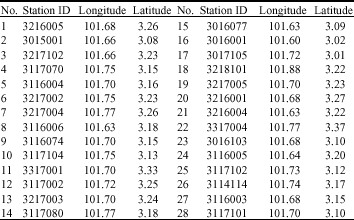
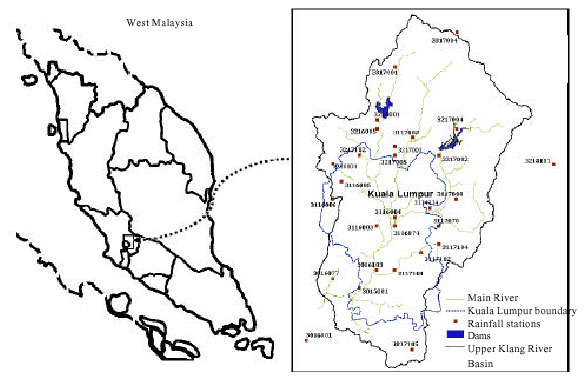
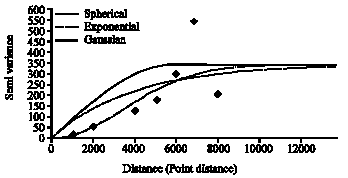
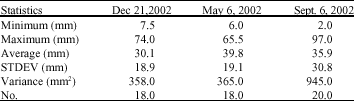
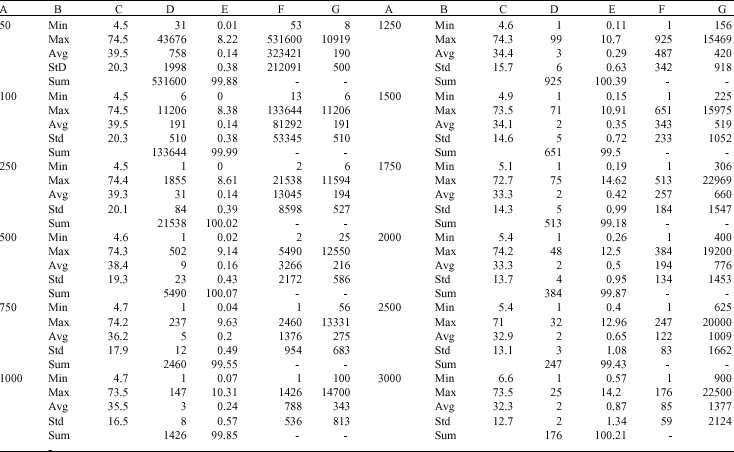
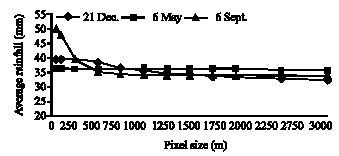
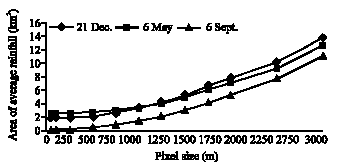
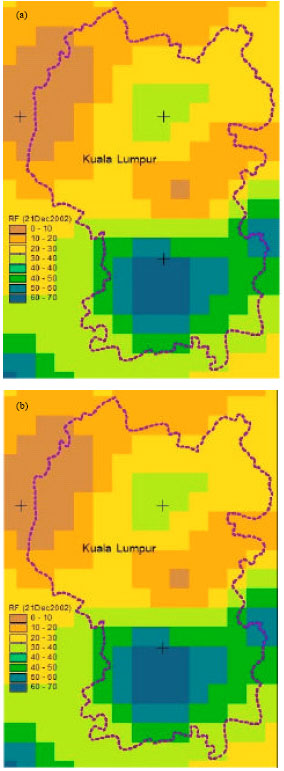
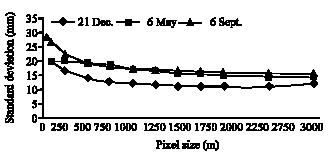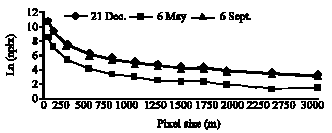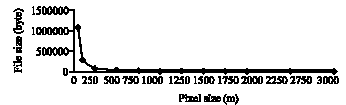Research Article
Effect of Pixel Size on the Areal Storm Pattern Analysis using Kriging
Department of Civil Engineering, University of Malaya, 50603 Kuala Lumpur, Malaysia
A. Abu Samah
Department of Civil Engineering, University of Malaya, 50603 Kuala Lumpur, Malaysia
F. Othman
Department of Civil Engineering, University of Malaya, 50603 Kuala Lumpur, Malaysia