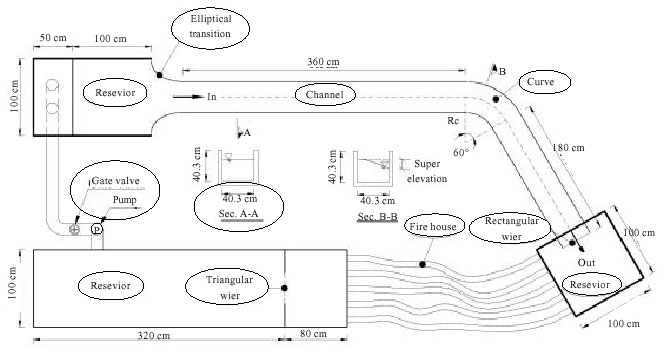
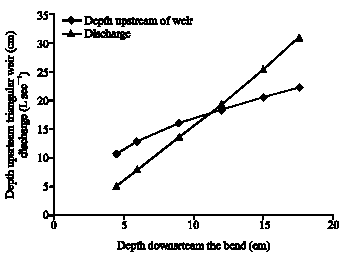
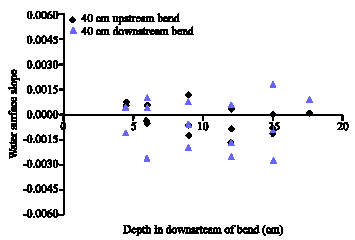
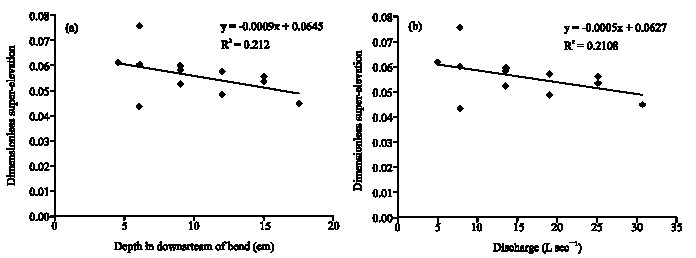
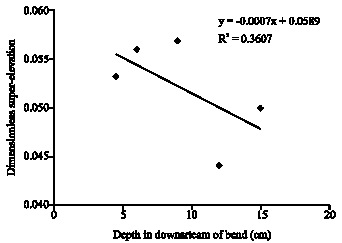
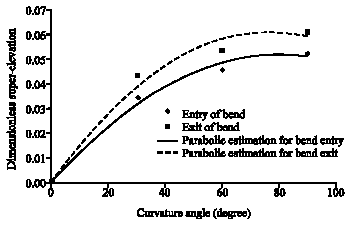
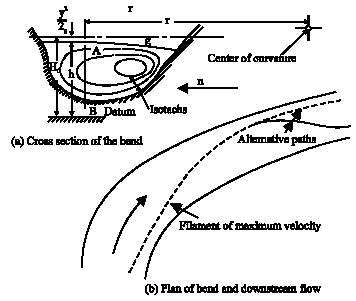
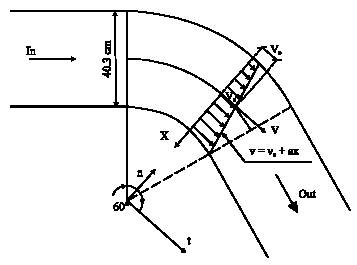
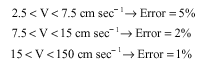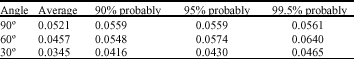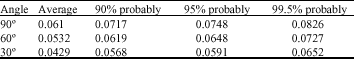Research Article
Experimental Investigations Water Surface Characteristics in Strongly-Curved Open Channels
Department of Civil Engineering, Ferdowsi University of Mashhad, 91775-1111, Iran
J. Abrishami
Department of Civil Engineering, Ferdowsi University of Mashhad, 91775-1111, Iran
M.B. Sharifi
Department of Civil Engineering, Ferdowsi University of Mashhad, 91775-1111, Iran