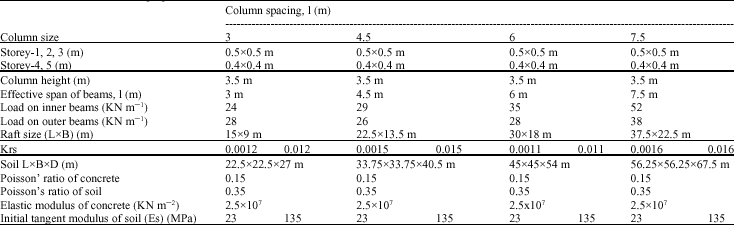
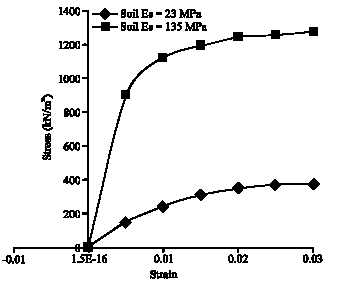
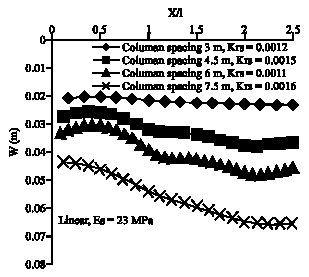
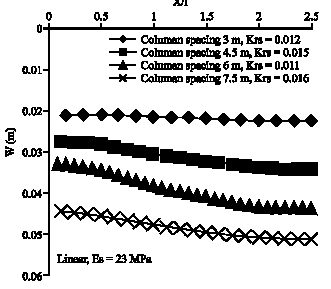
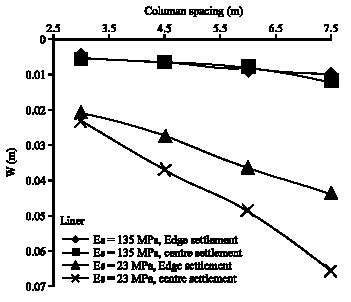
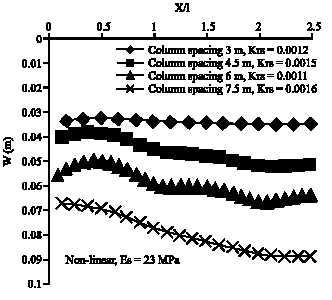
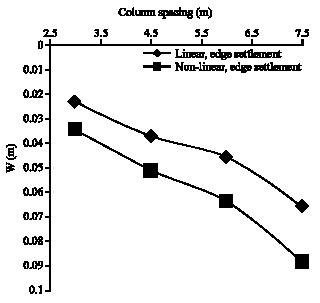
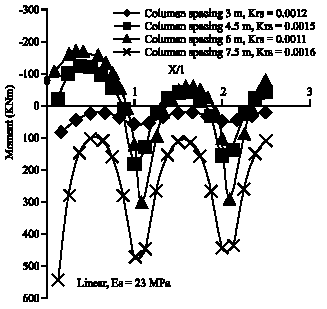
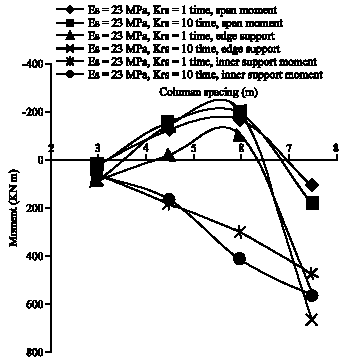
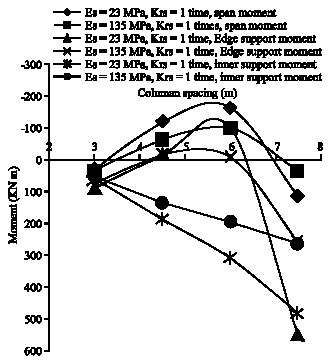
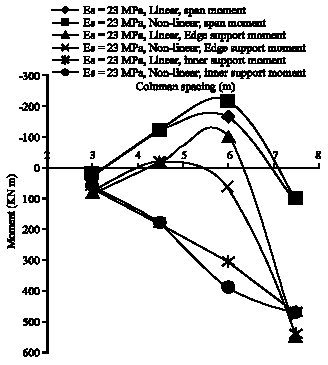
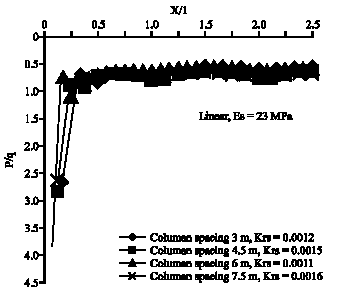
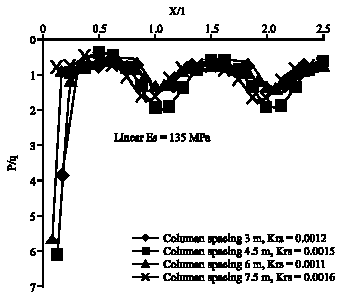
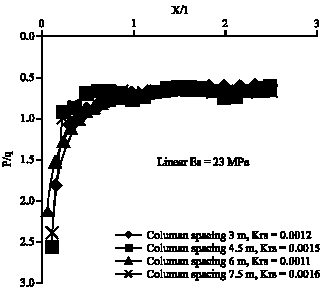
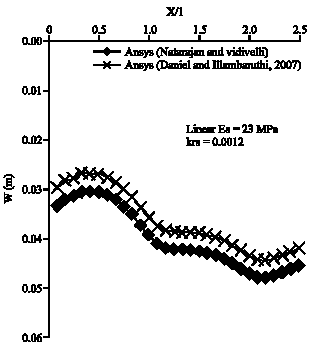
Research Article
Effect of Column Spacing on the Behavior of Frame-Raft and Soil Systems
Department of Structural Engg, Annamalai University, Annamalainagar-608002, India
B. Vidivelli
Department of Structural Engg, Annamalai University, Annamalainagar-608002, India