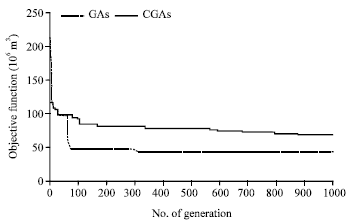
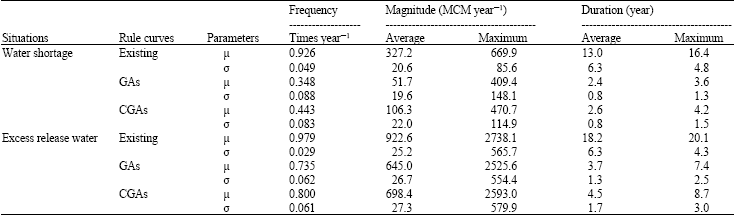
Research Article
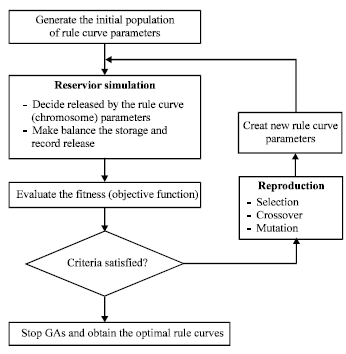
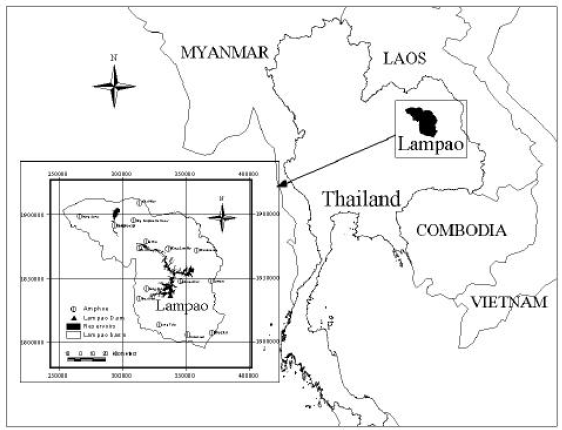
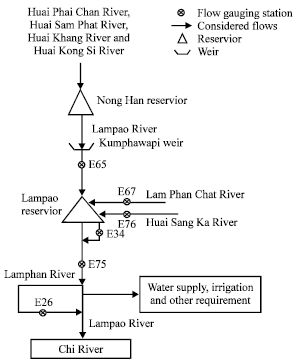
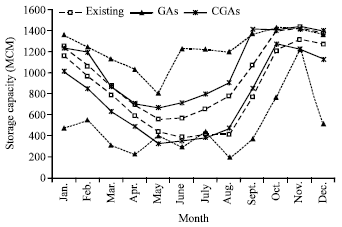
A Conditional Genetic Algorithm Model for Searching Optimal Reservoir Rule Curves
Faculty of Engineering, Mahasakham University, Thailand
A. Kangrang
Faculty of Engineering, Mahasakham University, Thailand
A. Lamom
Faculty of Engineering, Mahasakham University, Thailand
R. Hormwichian
Faculty of Engineering, Mahasakham University, Thailand
A. Kangrang
Faculty of Engineering, Mahasakham University, Thailand
A. Lamom
Faculty of Engineering, Mahasakham University, Thailand