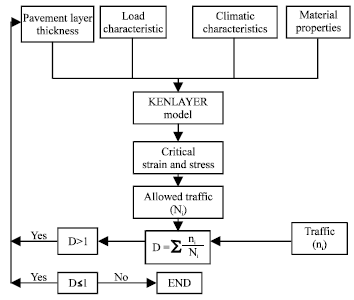
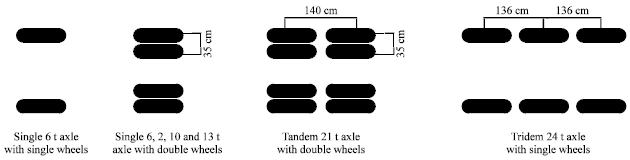
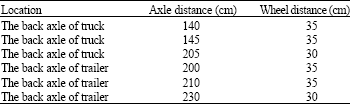
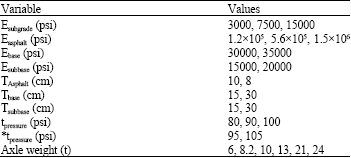
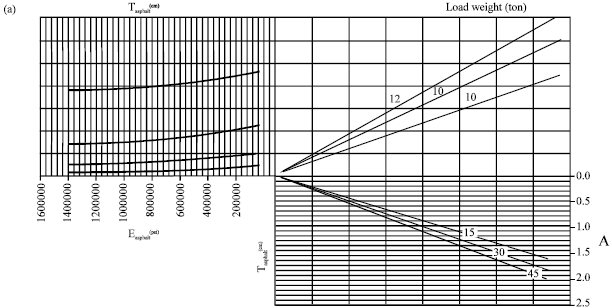
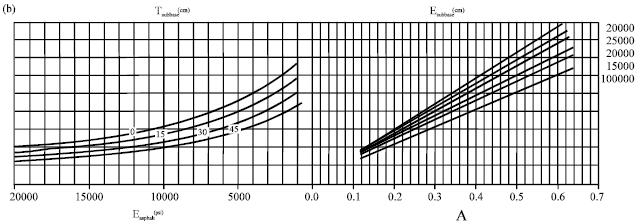
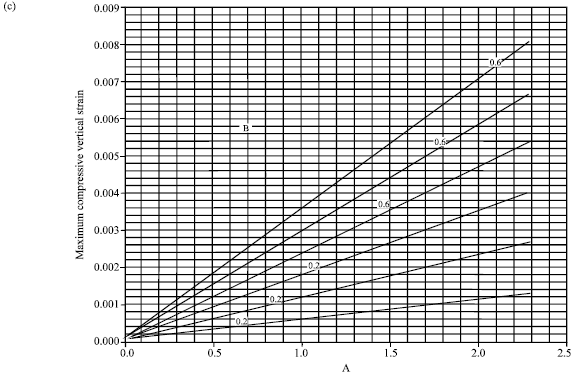
Research Article
Development of Mechanistic-Empirical Flexible Pavement Design in Iran
Department of Civil Engineering, University of Science and Technology, Tehran, Iran
A. Khavandi
Department of Civil Engineering, University of Science and Technology, Tehran, Iran