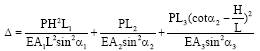Research Article
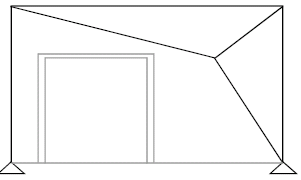
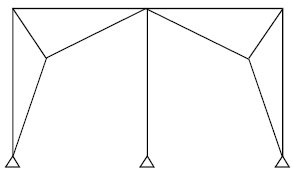
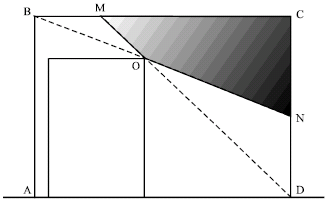
Eccentricity Optimization of NGB System by using Multi-Objective Genetic Algorithm
Department of Civil Engineering, Faculty of Engineering, University of Malaya, 50603 Kuala Lumpur, Malaysia
N.H. Ramli Sulong
Department of Civil Engineering, Faculty of Engineering, University of Malaya, 50603 Kuala Lumpur, Malaysia