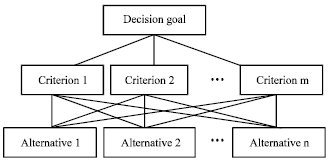
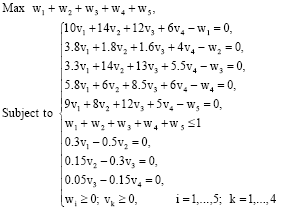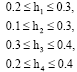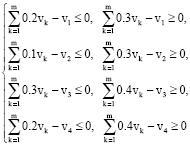Research Article
A New Method Based on Data Envelopment Analysis to Derive Weight Vector in the Group Analytic Hierarchy Process
Department of Industrial Engineering, Faculty of Engineering,Shahed University, P.O. Box 18155/159, Tehran, Iran
H. Navidi
Department of Mathematics, Shahed University, P.O. Box 18155/159, Tehran, Iran
A. Hajfathaliha
Department of Industrial Engineering, Faculty of Engineering,Shahed University, P.O. Box 18155/159, Tehran, Iran