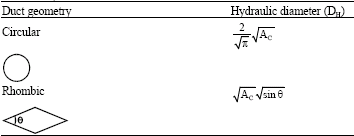Research Article
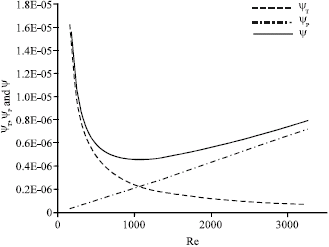
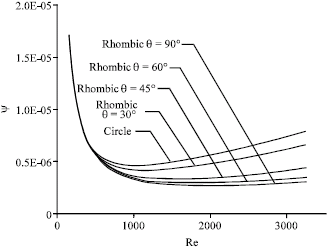
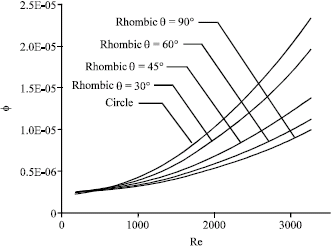
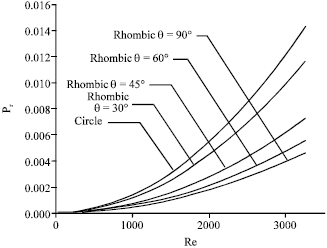
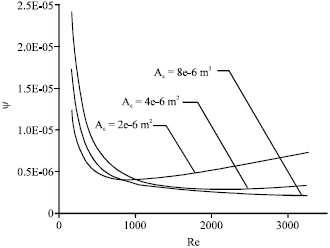
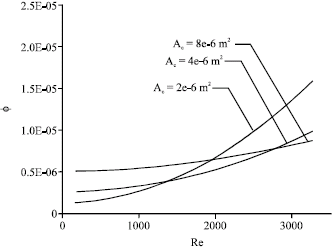
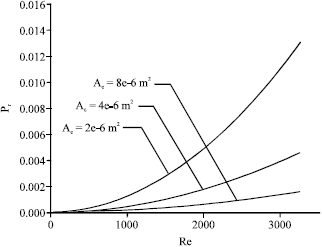
Irreversibilities in Duct Geometries of Rhombic and Circular with Constant Wall Heat Flux and Laminar Flow
Department of Mechanical Engineering, Babol Noshirvani University of Technology, P.O. Box 484, Babol, Iran
H. Mirgolbabaei
Department of Mechanical Engineering, KN Toosi University of Technology, Mollasadra, Tehran, Iran