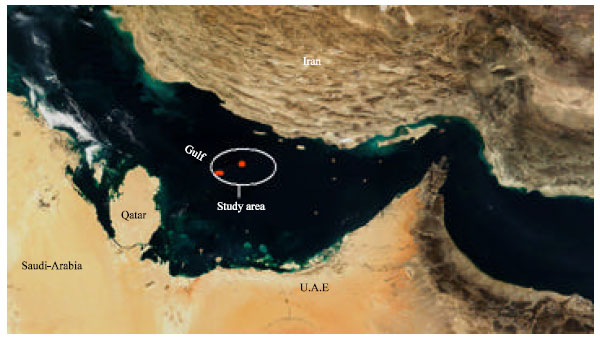
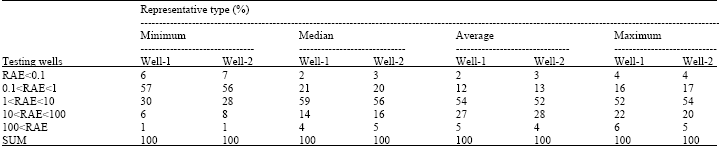
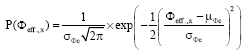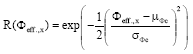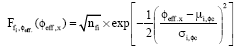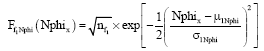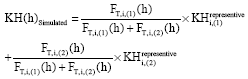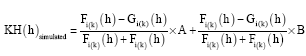Research Article
Permeability Prediction Enhancement in Carbonate Reservoirs by Proposing a New Fuzzy Logic Approach
Department of Mining, Metallurgical and Petroleum Engineering, Amir Kabir University of Technology, Tehran, Iran
M. Ali Riahi
Institute of Geophysics, University of Tehran, P.O. Box 14155-6466, Tehran, Iran
N. Alizadeh
Department of Mining, Metallurgical and Petroleum Engineering, Amir Kabir University of Technology, Tehran, Iran
M. Rezaei
NIOC, Pars Oil and Gas Co (POGC), Parvin St., Fatemi Blv, Tehran, Iran