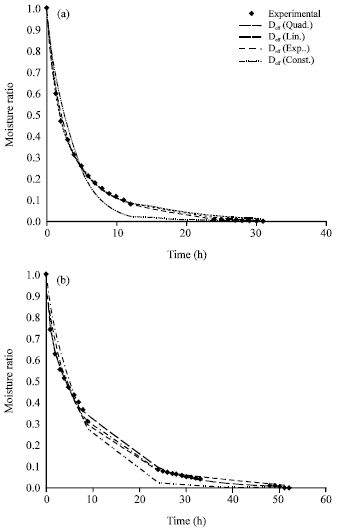
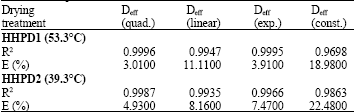
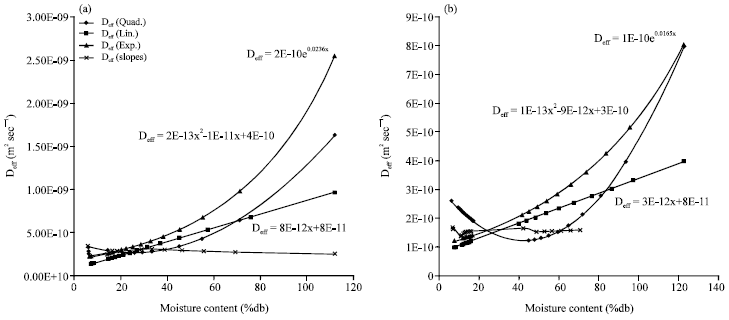
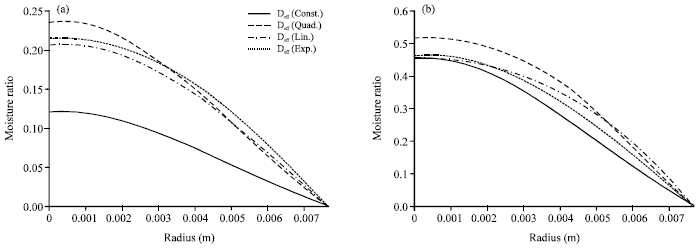
Research Article
Determination of Effective Diffusivity of Cocoa Beans using Variable Diffusivity Model
Department of Chemical and Environmental Engineering, University of Nottingham, Malaysia Campus Jalan Broga, 43500 Semenyih, Selangor Darul Ehsan, Malaysia
C.L. Law
Department of Chemical and Environmental Engineering, University of Nottingham, Malaysia Campus Jalan Broga, 43500 Semenyih, Selangor Darul Ehsan, Malaysia
M. Cloke
Department of Chemical and Environmental Engineering, University of Nottingham, Malaysia Campus Jalan Broga, 43500 Semenyih, Selangor Darul Ehsan, Malaysia