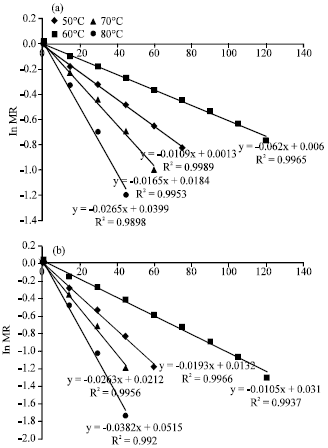
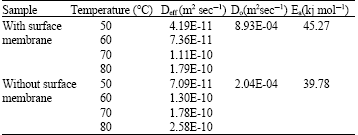
Research Article
Mathematical Modelling of Thin Layer Drying of Salak
Department of Chemical and Environmental Engineering, University of Nottingham, Malaysia Campus, Jalan Broga, 43500 Semenyih, Selangor Darul Ehsan, Malaysia
C.L. Law
Department of Chemical and Environmental Engineering, University of Nottingham, Malaysia Campus, Jalan Broga, 43500 Semenyih, Selangor Darul Ehsan, Malaysia