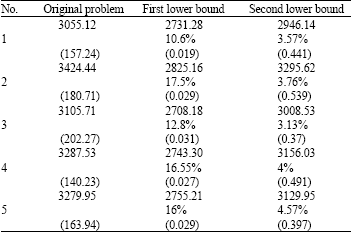
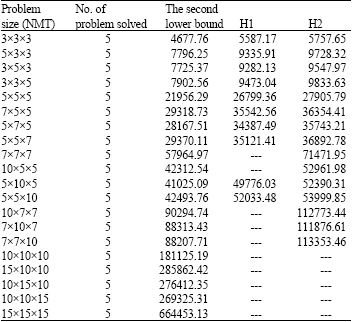
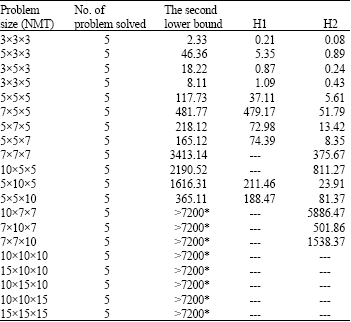
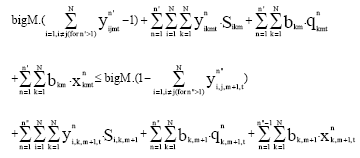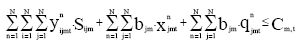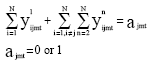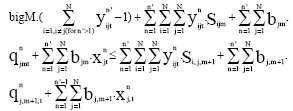Research Article
Development of Heuristics for Multi-Product Multi-Level Capacitated Lotsizing Problem with Sequence-Dependent Setups
Department of Industrial Engineering, Amirkabir University of Technology, 424 Hafez Avenue, Tehran, Iran
S. M.T. Fatemi Ghomi
Department of Industrial Engineering, Amirkabir University of Technology, 424 Hafez Avenue, Tehran, Iran
B. Karimi
Department of Industrial Engineering, Amirkabir University of Technology, 424 Hafez Avenue, Tehran, Iran
S. A.Torabi
Department of Industrial Engineering, College of Engineering, University of Tehran, Tehran, Iran