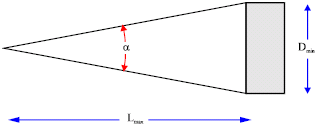
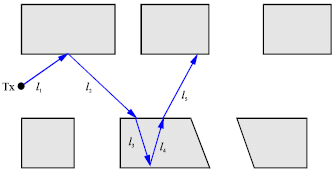
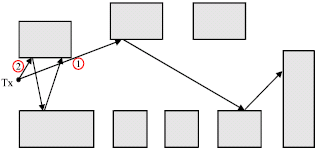
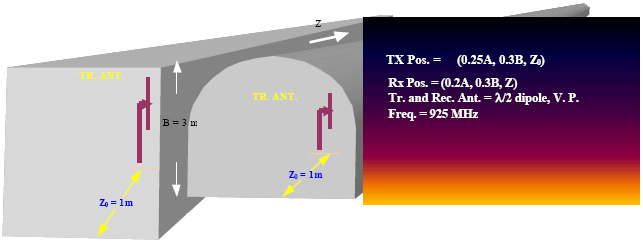
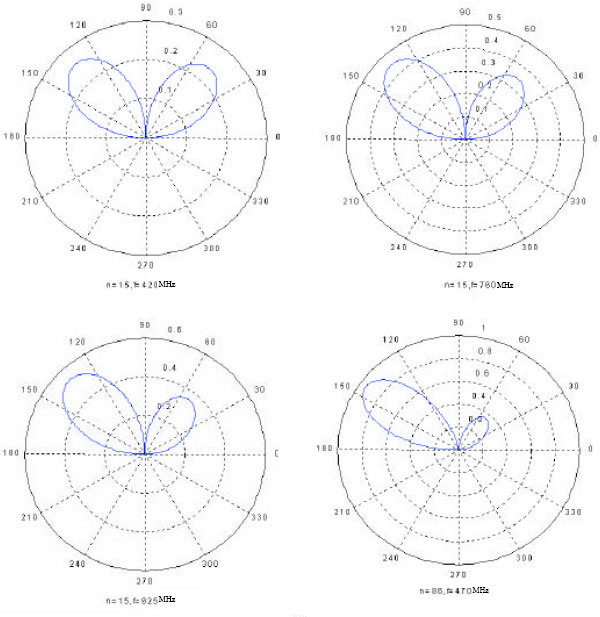
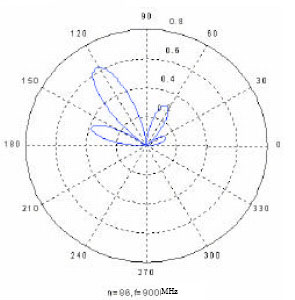
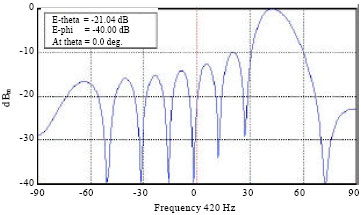
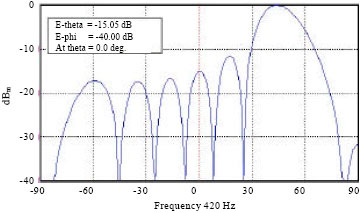
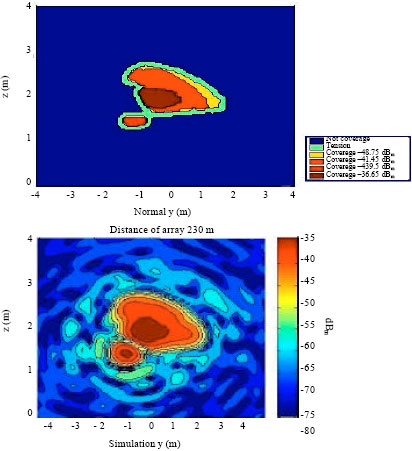
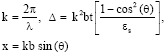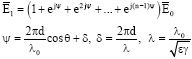Research Article
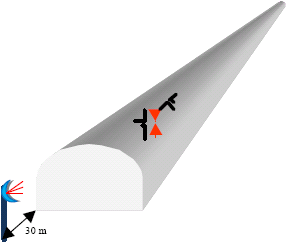
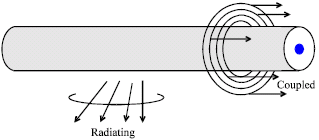
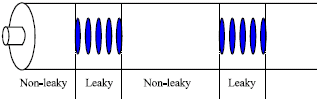
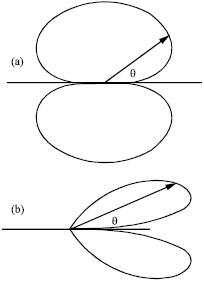
Radio Coverage inside Tunnel Utilizing Leaky Coaxial Cable Base Station
Department of Electrical, Electronic and Systems Engineering,Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor Darul Ehsan, Malaysia
M. Ismail
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment Building, Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor Darul Ehsan, Malaysia
N. Misran
Department of Electrical, Electronic and Systems Engineering, Faculty of Engineering and Built Environment Building, Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor Darul Ehsan, Malaysia
K. Jumari
Department of Electrical, Electronic and Systems Engineering,Faculty of Engineering and Built Environment Building, Universiti Kebangsaan Malaysia, 43600 UKM Bangi, Selangor Darul Ehsan, Malaysia