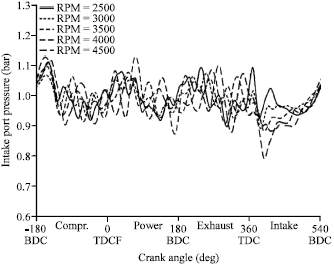
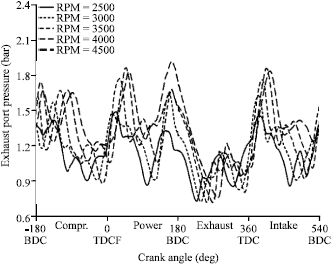
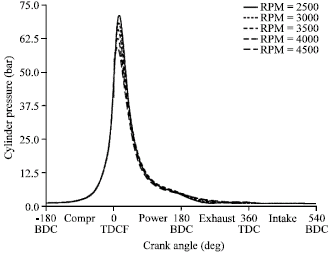
Research Article
Air Fuel Ratio on Engine Performance and Instantaneous Behavior of Crank Angle for Four Cylinder Direct Injection Hydrogen Fueled Engine
Automotive Excellence Center, Faculty of Mechanical Engineering, Universiti Malaysia Pahang, Tun Abdul Razak Highway, 26300 Gambang, Kuantan, Pahang, Malaysia
M. K. Mohammed
Automotive Excellence Center, Faculty of Mechanical Engineering, Universiti Malaysia Pahang, Tun Abdul Razak Highway, 26300 Gambang, Kuantan, Pahang, Malaysia
R. A. Bakar
Automotive Excellence Center, Faculty of Mechanical Engineering, Universiti Malaysia Pahang, Tun Abdul Razak Highway, 26300 Gambang, Kuantan, Pahang, Malaysia