Research Article
Land Use Scenarios and Optimization in a Watershed
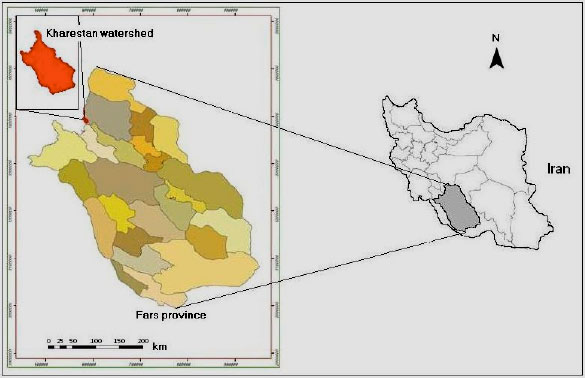
Soil Conservation and Watershed Management Research Institute, P.O. Box 13445-1136, Tehran, Iran
M. Shabani
Arsanjan Unit, Azad University, Fars, Iran
H. Ahmadi
Faculty of Natural Resources, Tehran University, Tehran, Iran