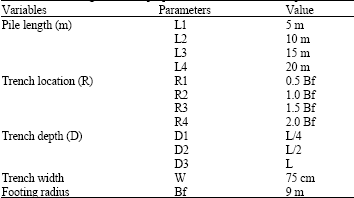
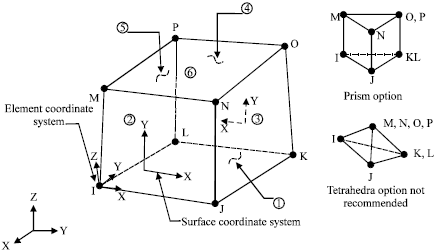
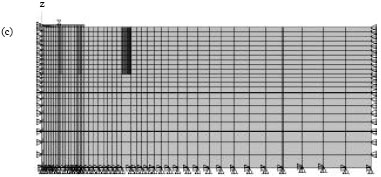
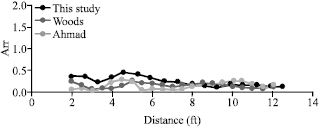
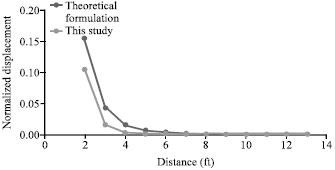
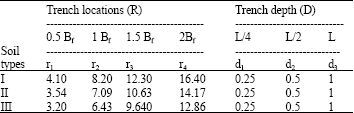
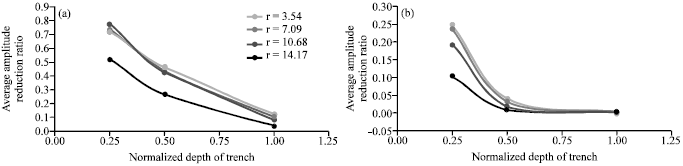
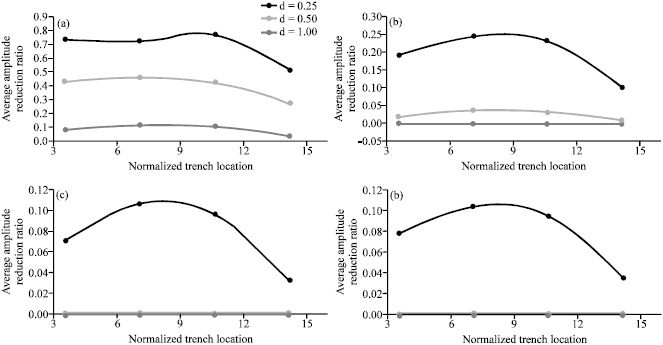
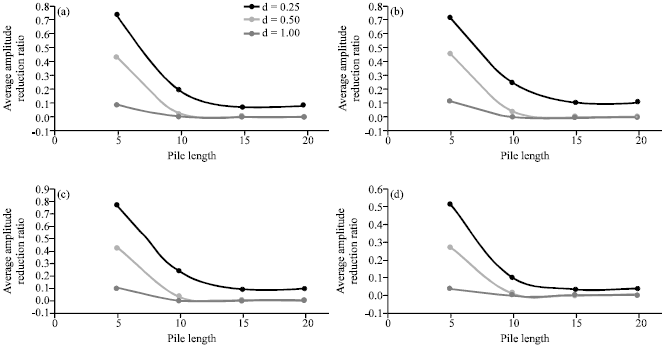
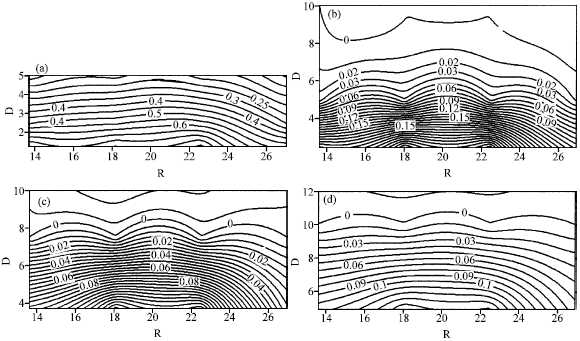
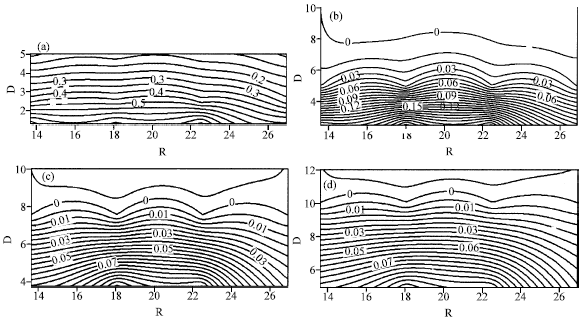
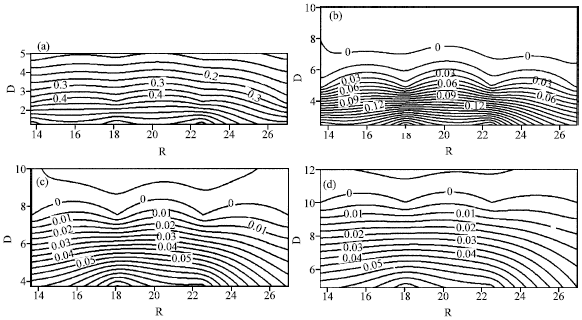
Research Article
Three Dimensional Analysis of Active Isolation of Deep Foundations by Open Rectangular Trenches
Department of Civil Engineering, Imam Khomeini International University, P.O. Box 288, Qazvin, Iran
M.R. Shafie
Department of Civil Engineering, Imam Khomeini International University, P.O. Box 288, Qazvin, Iran
R.S. Vileh
Consultant Engineer, Adelaide, Australia