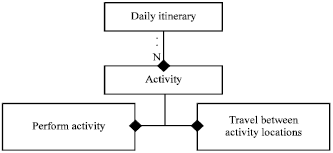
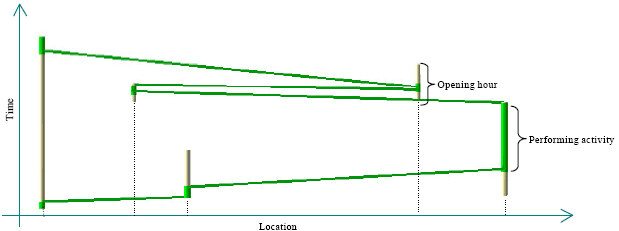
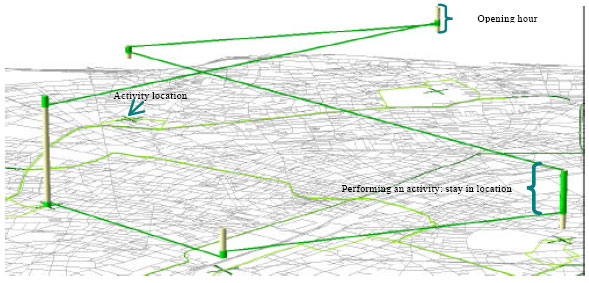
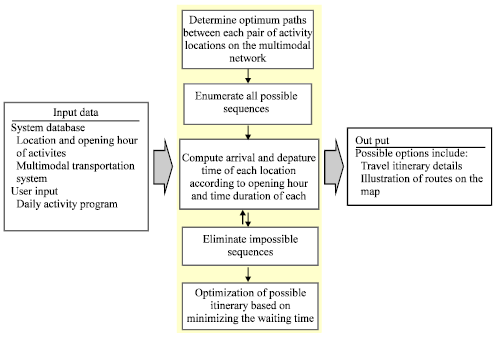
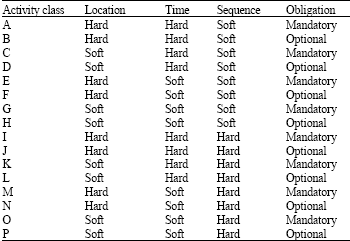
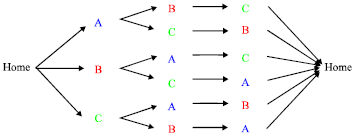
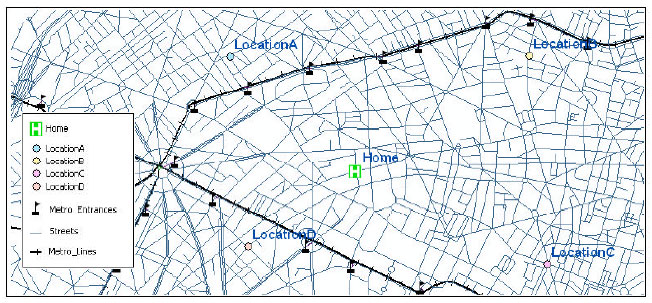
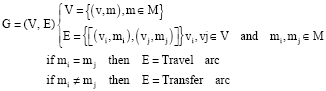Research Article
Travel Itinerary Planning in Public Transportation Network Using Activity-Based Modeling
GIS Division, Department of Surveying and Geomatics Engineering, College of Engineering, University of Tehran, Tehran, Iran
M.R. Delavar
Center of Excellence in Geomatics Engineering and Disaster Management, Department of Surveying and Geomatics Engineering, College of Engineering, University of Tehran, Tehran, Iran
M.R. Malek
Department of GIS, Faculty of Geodesy and Geomatics Engineering, KN Toosi University of Technology, Tehran, Iran