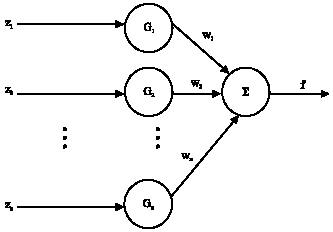
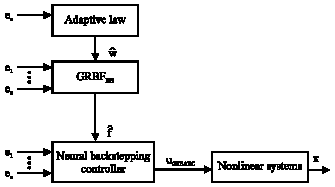
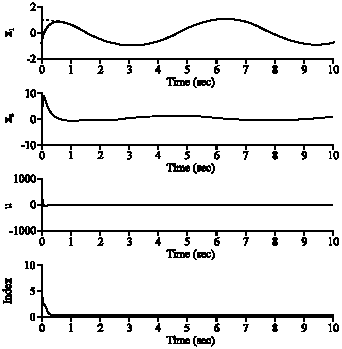
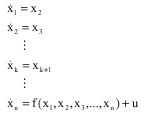Research Article
Gaussian Radial Basis Adaptive Backstepping Control for a Class of Nonlinear Systems
Department of Mechatronics Engineering, The Islamic Azad University, Science and Research Branch, Tehran, Iran
M. Aliyari Shoorehdeli
Department of Electrical Engineering, KNT University of Technology, Tehran, Iran
M.A. Nekoui
Department of Electrical Engineering, KNT University of Technology, Tehran, Iran
M. Teshnehlab
Department of Electrical Engineering, KNT University of Technology, Tehran, Iran