Research Article
Module Approximate Amenability for Semigroup Algebras
Department of Mathematics, Persian Gulf University, Boushehr, 75168, Iran
Hashem Najafi
Department of Mathematics, Persian Gulf University, Boushehr, 75168, Iran
New notions of amenability was introduced by Amini (2004) and Ghahramani and Loy (2004). In this study, we mix these different notions and introduce module approximate amenability for a Banach algebra and then we investigate this notion on semigroup algebra l1 (S).
Let A be a Banach algebra and X be a Banach A-bimodule. A derivation from A into X is a bounded linear map D:A → X satisfying:
D(ab) =a.D(b)+D(a).b |
For each xεX we denote by adx the derivation D(a) = ax-xa for all aεA, which is called an inner derivation. If X is a Banach A-bimodule, X* (the dual space of X) is an A-bimodule as usual. A Banach algebra A is called amenable if for any Banach A-bimodule X, every derivation D : A→X* is inner. The celebrated Johnson’s Theorem (in discrete case) asserts that a discrete group G is amenable if and only if the Banach algebra l1(G) is amenable (Johnson, 1972).
A Banach algebra A is called approximately amenable if for any Banach A-bimodule X, every derivation D : A→X* is approximately inner, that is, there exists a net (fi)fX* such that for every aεA, ![]() in norm topology. Approximate amenability was introduced by Ghahramani and Loy (2004). One of motivations for definition of approximate amenability comes from Gourdeau (1992), where the researchers has shown that the assumption of existence of a bounded net (xi) is in fact equivalent to amenability of A.
in norm topology. Approximate amenability was introduced by Ghahramani and Loy (2004). One of motivations for definition of approximate amenability comes from Gourdeau (1992), where the researchers has shown that the assumption of existence of a bounded net (xi) is in fact equivalent to amenability of A.
Let U and A be Banach algebras such that A is a Banach U-bimodule with compatible actions, that is:
Let X be a Banach A-bimodule and a Banach U-bimodule with compatible actions, that is:
and the same for right or two-sided action. Then we say that X is a Banach A-U-module. Moreover, if:
then X is called a commutative A-U-module. A bounded map D : A→X is called a module derivation if:
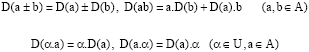 |
When, X is commutative, each xεX defines a module derivation as follows:
that is called inner derivation. Now we define module approximate amenability.
Definition 1: A Bananch algebra A, which is a U-bimodule, is called module approximately amenable (as a U-bimodule) if for any commutative Banach A-U-module X, each module derivation D : A→X* is approximately inner.
MODULE APPROXIMATE AMENABILITY FOR SEMIGROUP ALGEBRA
Here, we investigate module approximate amenability of l1(S) as a l1(E)-module, where, S is an inverse semigroup with idempotents E.
A discrete semigroup S is called an inverse semigroup if for each sεS there is a unique s*εS such that s*ss* = s* and ss* s = s. An element e ε S is called an idempotent if e2 = e* = e. The set of idempotent elements of S is denoted by E. It is easy to see that E is a commutative subsemigroup of S and l1(E) could be regarded as a subalgebra of l1 (S) (Howie, 1976).
We consider l1(S) as a l1(E)-module with the following module actions:
Consider the congruence relation ~ on S where, s~t if and only if there is an eεE such that se = te. The quotient semigroup GS:=S/~ is then a group. The inverse semigroup S is amenable if and only if the discrete group GS is amenable (Duncan and Namioka, 1978). With this notation, l1(GS) is a quotient of l1(S) and so the earlier action of l1(E) on l1(S) lifts to an action of l1(E) on l1(GS) and making it a Banach l1(E)-module.
Lemma 1: With above notations l1(GS) is module approximately amenable if and only if it is approximately amenable.
Proof: Consider the quotient map π:S→GS, that maps each sεS into congruence class of s. For each sεS and eεE we have π(s) = π(se) and so:
Thus action of l1(E) on l1(GS) is trivial. Therefore, we can take all Banach l1(GS)-modules as a commutative l1(GS)- l1(E)-module with trivial action of l1(E). Let X be a Banach l1(GS)-module and D : l1(GS)→X* be a module derivation. For each λεC (the field of complex numbers), fε l1(GS) and eεE we have:
This shows that D is C-linear. Hence, l1(GS) is module approximately amenable if and only if it is approximately amenable.
Theorem 1: Let A and B be Banach algebras and Banach U-modules with compatible actions and let φ:A→B be a continuous Banach algebra homomorphism and U-module homomorphism with dense range. If A is module approximately amenable, then so is A.
Proof: If X is a commutative B-U-module, it could be regarded as a commutative A-U-module by:
Also each module derivation D:B→X* gives a module derivation Doφ:A→X*. Since, A is module approximately amenable, there is a net (fi)fX* such that:
Since, a.fi = φ(a).fi and fi.a = fiφ.(a), we have:
Now density of φ(A) in B and continuity of D imply that:
Hence, B is module approximately amenable.
Theorem 2: Let S be an inverse semigroup with idempotents E. Consider l1(S) as a Banach module over l1(E) with the multiplication right action and the trivial left action. Then l1(S) is module approximately amenable if and only if S is amenable.
Proof: If S is amenable, then l1(S) is module amenable by Theorem 3.1 (Amini, 2004). Thus l1(S) is module approximately amenable. Conversely, let l1(S) be module approximately amenable. Consider the quotient map π:S→GS, that maps each sεS into congruence class of s. Then π induces the continuous epimorphism ![]() . The earlier theorem shows that l1(GS) is module approximately amenable and so l1(GS) is approximately amenable by Lemma 1. Hence GS is amenable group by Theorem 3.2 by Ghahramani and Loy (2004). Therefore, S is amenable by Theorem 1 by Duncan and Namioka (1978).
. The earlier theorem shows that l1(GS) is module approximately amenable and so l1(GS) is approximately amenable by Lemma 1. Hence GS is amenable group by Theorem 3.2 by Ghahramani and Loy (2004). Therefore, S is amenable by Theorem 1 by Duncan and Namioka (1978).
Remark: Lashkarizadeh and Samea (2005) have shown that if S is a cancellative semigroup such that l1(S) is approximately amenable, then S is amenable.
The authors would like to thank the Persian Gulf University Research Council for their financial support.