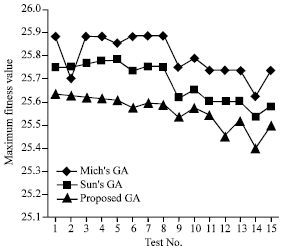
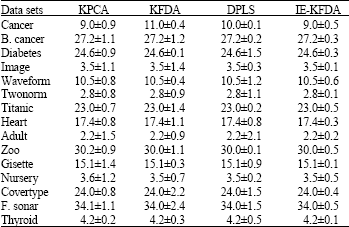
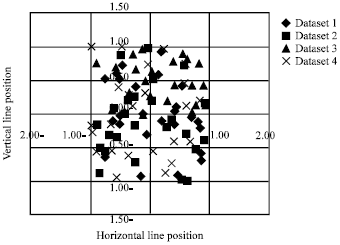
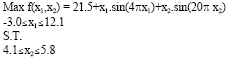Research Article
Improved Evolving Kernel of Fisher’s Discriminant Analysis for Classification Problem
Department of Intelligent Systems Engineering, Okayama University, 1-1 Tsushima Naka 3-chome, 700-8530 Okayama, Japan
Hossam A. Gabbar
Faculty of Energy Systems and Nuclear Science, UOIT, ON L1H 7K4 Ontario, Canada
Shigeji Miyazaki
Department of Intelligent Systems Engineering, Okayama University, 1-1 Tsushima Naka 3-chome, 700-8530 Okayama, Japan