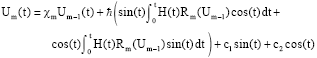Research Article
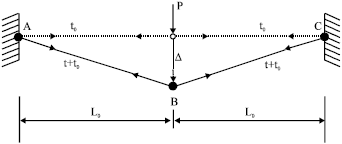
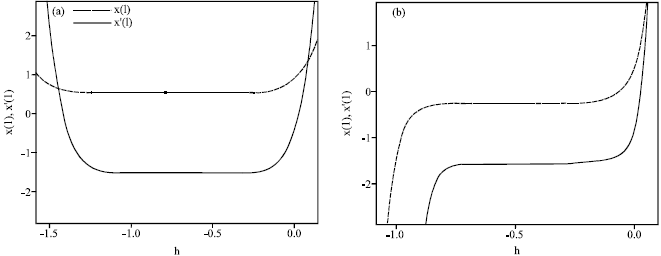
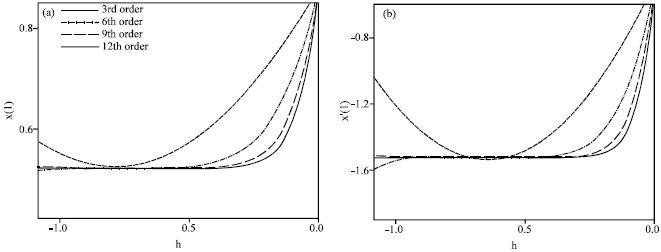
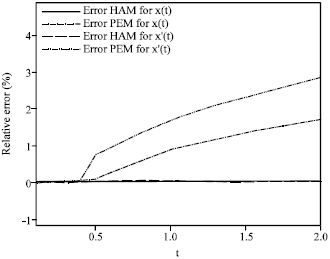
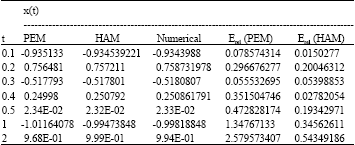
Assessment of HAM and PEM to Find Analytical Solution for Calculating Displacement Functions of Geometrically Nonlinear Prestressed Cable Structures with Concentrated Mass
Department of Mechanical Engineering, Islamic Azad University, Dezful Branch, Dezful, Khozestan, Iran
E. Rokni
Department of Mechanical Engineering, Shahid Bahonar University of Kerman, Kerman, Iran
A. Kimiaeifar
Department of Mechanical Engineering, Shahid Bahonar University of Kerman, Kerman, Iran
M. Rahimpour
Department of Mechanical Engineering, Shahid Bahonar University of Kerman, Kerman, Iran