ABSTRACT
This study presents a new method for calculating the optimal bidding strategies among Generating Companies (GENCOs) in the electricity markets with the assumptions of imperfect competition and complete information and with consideration of uncertainty in load forecast. The parameterized Supply Function Equilibrium (SFE) is employed for modeling the imperfect competition among GENCOs in which proportionate parameterization of the sole and the intercept is used. A pay-as-LMP pricing mechanism is assumed for settling the market and calculating the GENCOs’ profits. The fuzzy approach is utilized for modeling the uncertainty of load forecast and the result is compared with probabilistic approach. A nine GENCOs test system is used to show the efficiency of the proposed method.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2009.2218.2227
URL: https://scialert.net/abstract/?doi=jas.2009.2218.2227
INTRODUCTION
In recent decades, the electricity supply industry throughout the world has been moved from nationalized monopolies into competitive markets. Electricity is evolving into a distributed commodity in which market forces are bound to drive its price and reduce the net cost through increased competition. In such a market, the existence of an independent entity called Independent System Operator (ISO) is necessary. The ISO is a regulatory organization and one of its responsibilities is to balance the network in a manner that maximizes the welfare of the industry as a whole (Kirschen and Strbac, 2004; Shahidehpour et al., 2002).
In a restructured electricity market, each Generating Company (GENCO) submits bids to the ISO with the goal of maximizing its own benefits. So, each GENCO tries to establish a suitable bidding strategy to maximize its potential profit (David and Wen, 2000). Finding the optimal bidding strategy of GENCOs depends on the type of competition. In the perfect competition, all of the market participants are called price takers and don’t have the ability to influence the market price through their individual actions. Developing bidding strategy in perfect competition is based on price forecasting. Forecasted price will be used in a Price-Based Unit Commitment (PBUC) program for determining the bid that maximizes profit. In Arroyo and Conejo (2000), Li et al. (2002) and Li and Shahidehpour (2005b) a deterministic PBUC was applied for developing bidding strategies. But due to the uncertainty in equipment outages, fuel prices and other price drivers, it could be difficult to forecast market prices accurately (Amjady and Hemmati, 2006). However, because of direct impact of the precision of market price forecasting on PBUC solution, it would be very important to consider the market price uncertainty. Mont-Carlo Simulation (MCS) is utilized (Li et al., 2007) to generate a set of discrete (deterministic) market prices based on forecasted market prices and then the bidding curve is constructed with the goal of maximizing the expected payoff.
There are several approaches to analyze the problem of developing optimal bidding strategy in electricity markets with imperfect competition. They could be categorized into non-equilibrium and equilibrium models (Li et al., 2007). The basic idea in non-equilibrium models is to use an approximate model for analyzing the impact of a GENCO’s bidding strategies on market clearing price. For example, an ordinal optimization method was used (Guan et al., 2001) to find the good enough bidding strategy for power suppliers. In equilibrium models, game theory concepts are utilized to simulate bidding behaviors of GENCOs. The solution of this game, if it exists, is the optimal bidding strategy of each GENCO and represents a market Nash Equilibrium (NE) which means that each GENCO’s profit will reduce if it unilaterally changes its bidding strategy while other GENCO’s bidding strategy remain fixed. If there is no collusion and each player’s payoff are known to all players, then the optimal bidding strategy problem could be considered as a non-cooperative game with complete information.
In recent research, the strategic bidding problem is formulated as a bilevel optimization problem using the Supply Function Equilibrium (SFE) model for modeling the imperfect competition among GENCOs. In this bilevel optimization problem, the upper level sub-problem maximizes the individual GENCOs’ payoffs and the lower sub-problem (convex quadratic programming) solves the ISO’s market clearing problem. Weber and Overbye (2002) represented the problem as a bilevel optimization problem and utilized price and dispatch sensitivity information, available from the OPF solution, to determine how a market participant should vary its bid in order to increase its profit. Via a bilevel optimization technique and Karush-Kuhn-Tucker (KKT) complementary conditions, Hobbs et al. (2000) transformed the strategic bidding problem to a nonlinear programming model or, more specifically, to a mathematical program involving linear complementary constraints. Also Li and Shahidepour (2005a) utilized the primal-dual interior point method and sensitivity functions to solve this bilevel problem.
One of the common uncertainties in equilibrium models of imperfect competition markets is the uncertainty of load forecasting. In fact, forecasted load has the direct impact on the solution of the game and it will be very important to be considered. There are two approaches to handle this uncertainty: probabilistic approach and fuzzy approach.
In this study, a fuzzy approach for modeling the uncertainty of load forecast in imperfect competition market is developed and its result is compared to probabilistic approach. In probabilistic approach, it’s assumed that future demand is normally distributed and each player attempts to solve a Chance Constrained Problem (CCP) (Chouchman et al., 2005). In fuzzy approach, possibility distributions are used for demand values in the future (Rosado and Navarrov, 2004; Popovic and Popovic, 2004) and fuzzy game theory is utilized for developing the optimal bidding strategy of each GENCO. Also, the bilevel optimization model, applied by Li and Shahidepour (2005a), or equivalently, the Mathematical Problem with Equilibrium Constraints (MPEC) model applied by Hobbs et al. (2000), is employed for developing optimal bidding strategy for competitor suppliers participating in the Day-Ahead (DA) energy market. In this market, it’s supposed that the ISO uses a DC Optimal Power Flow (DC OPF) to clear the market after collecting bids and pays the suppliers under pay-as-LMP pricing. Suppliers are assumed to bid affine non-decreasing supply curve. Strategic behavior is represented via a parameterized SFE model and the x α y parameterization technique is considered for the SFE model in which the suppliers can manipulate the slope and the intercept proportionally.
Market assumption: Here, supply curves of the energy are restricted to be affine and non-decreasing. An SFE model is adopted to represent the strategic behavior of the suppliers. If an SFE model is chosen, then the supply function is in the form of x + y · P. Each GENCO can choose different values for x and y which are referred to as strategic variables. Four parameterization techniques for strategic variables are considered, including x parameterization, y parameterization, x α y parameterization and x, y parameterization. Baldick (2002) showed that the parameterization effect on the market results is significant. For simplicity, it’s supposed that each GENCO has an equivalent cost function of its own generators and will submit a bid to the ISO according to the following linear supply function (Wood and Wollenberg, 1996):
(1) |
where, Bid (Pi) is bidding price of GENCO I for producing the power of Pi and ki is bidding strategy of GENCO I (a real number). The value of ki is close to 1 for price takers in equilibrium points.
Market clearing mechanism (lower level sub-problem): The market clearing mechanism is based on the maximization of the declared social welfare, or equivalently, the minimization of the consumer payments subject to transmission and suppliers physical constraints. Accordingly, Locational Marginal Prices (LMPs) are calculated as:
(2) |
s.t.
(3) |
(4) |
(5) |
(6) |
where, Eq. 2 represents the total cost of providing energy which depends on the bids submitted by the suppliers. Equation 3-4 state the Kirchhoff’s current and voltage laws, respectively (DC load flow formulation). Equation 5-6 specify the supplier capacity and the line limits, respectively. To avoid non-convexities in Eq. 2-6 due to 0-1 Unit Commitment (UC) decisions, the suppliers are assumed to take the 0-1 states as given based on the UC results (Haghighat et al., 2007).
Forming the KKT conditions (Wood and Wollenberg, 1996) for the primal problem Eq. 2-6 and using dual variables μ, π, λ and γ, the following nonlinear complementary formulation of the primal problem (by dropping indices) is obtained:
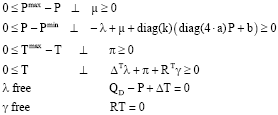 | (7) |
where, matrices Δ and R were introduced earlier.
After solving Eq.7 with respect to the strategy of each GENCO and calculating the dual variables, the following results will be obtained.
Lemma 1: The LMP and accepted power of each GENCO can be stated as:
(8) |
(9) |
where, ki is the strategy of ith GENCO and Ai, Bi and LDi, are parameters which depend on other GENCOs’ strategies (k–I) and have different values for different states of reaching a generation or transmission constraint.
With the assumption of the network lines have large enough capacity, the expressions for Ai, Bi and LDi, would be as follows (These are proved in Appendix):
 | (10) |
All GENCOs in cap+ and cap– sets should produce their maximum and minimum capacity, respectively. According to Eq. 10, the strategies of these GENCOs don’t have any effect on LMPs and accepted power of other GENCOs that aren’t in cap set.
Supplier problem (upper level sub-problem): The problem faced by each player is the maximization of its profit where profit comprises the difference between revenue and production cost. The cost of producing energy is calculated as:
(11) |
The revenue of the supplier is the revenue of selling energy in the market and can be calculated under a pay-as-LMP scheme as:
(12) |
The supplier payoff (profit) is revenue minus cost, namely:
(13) |
Using the results of the market clearing problem and inserting the calculated LMPi and Pi in Eq. 1, the supplier payoff can be written with respect to its strategy (ki) as:
(14) |
After some manipulation, we have:
(15) |
Where:
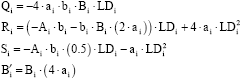 |
Thus, the supplier problem is transformed from the bilevel optimization problem (or the MPEC problem) to the following one level optimization problem:
(16) |
where, the impact of the ISO and the rivals’ actions are observed through the Ai, Bi and Ldi.
Complete information gaming: In an electricity market, each GENCO tries to maximize its own profit as shown in Eq. 16, thus by equating the first derivative of the profit with respect to its strategy (ki) to zero (i.e., the necessary conditions for maximization), its optimal strategy will be calculated as:
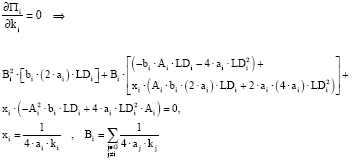 | (17) |
The sufficient conditions for maximization will be reached, if the solution found in Eq. 17 satisfies the following inequality:
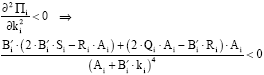 | (18) |
where, Qi, Ri and Si, are defined in Eq. 15.
Finally for computing the Nash equilibrium of the market through utilizing game theory technique, we can state the problem as an n-player game. There are n players in the game that they simultaneously play with their own bidding strategies. Therefore, a NE will be calculated from solving n equations similar to Eq. 17 for all players simultaneously and the solution of this set of equations means that no player will have incentive to unilaterally change its bidding strategy.
UNCERTAINTY MODELS OF LOAD FORECAST
Two fundamental models to handle the uncertainty of load forecasting are possibilistic (fuzzy) and probabilistic models that are presented.
Possibilistic model: In this approach, it’s supposed that the uncertainty in load forecasting is represented as a Triangular Fuzzy Number (TFN). Then, the profit of each GENCO will be computed as a fuzzy number. The fuzzy game theory is utilized for determining the optimal bidding strategy.
Fuzzy uncertainty: In fuzzy set theory, each object x in a fuzzy set X is given a membership value using a membership function denoted by μ(x), which is corresponding to the characteristic function of the crisp set whose values range between zero and one. In fuzzy sets, the closer the value μ(x) to 1, the more x belongs to X. Fuzzy sets are defined as functions that map a member of the set to a number between 0 and 1, indicating its actual degree of membership as means to model the uncertainty of natural language.
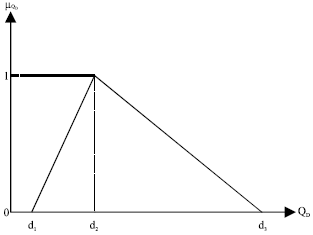
One of the major uncertainties associated with the strategic bidding problem is the uncertainty in the load forecast. Typically, the load forecast is subject to ±(2-3)% error (Shahidehpour et al., 2002). The power demand at each bus can be represented using a value d1 (the pessimistic value of demand), a value d3 (the optimistic value of demand) and a value d2 (the possibilistic value of demand that corresponds to the value 1 of the membership function μ), as shown in Fig. 1.
This description of the demand is associated with a triangular possibility (fuzzy) distribution, ![]() (Rosado and Navarrov, 2004; Popovic and Popovic, 2004) and represents simultaneously a large set of possible future demand values at a given bus.
(Rosado and Navarrov, 2004; Popovic and Popovic, 2004) and represents simultaneously a large set of possible future demand values at a given bus.
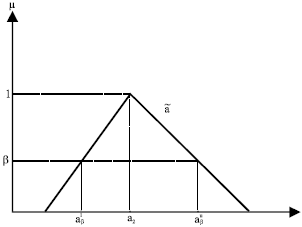
Comparison of objective function values: When the power demand has possibility distribution with triangular membership function, thus the nonlinear objective functions (GENCOs’ payoffs functions) have possibility distribution. These fuzzy values must be compared and ranked to assess solutions. The ranking function removal (Lai and Hwang, 1992) allows comparison between these values. The removal of a fuzzy number ã for a Bender cut of magnitude β is defined as (Fig. 2):
(19) |
To compare two fuzzy values ã and ![]() their removal values will be compared. For example, in Fig. 3, for the minimal acceptance degree β and for every Bender cut greater than β, the inequality
their removal values will be compared. For example, in Fig. 3, for the minimal acceptance degree β and for every Bender cut greater than β, the inequality ![]() will be valid.
will be valid.
Linearity is one of the main properties of removal function. For example, if fuzzy value ![]() is composed of two fuzzy values as
is composed of two fuzzy values as ![]() then after applying removal function, we have:
then after applying removal function, we have:
 | |
| Fig. 1: | Fuzzy representation of power demand |
 | |
| Fig. 2: | Bender cut of magnitude β of a triangular fuzzy number |
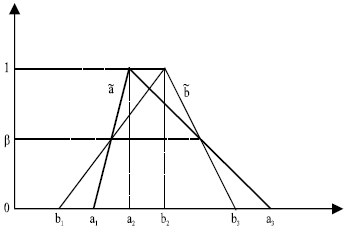 | |
| Fig. 3: | ã is preferred to |
(20) |
Fuzzy constraints: By modeling loads as fuzzy numbers, the accepted power and the power flow of lines are translated into the fuzzy domain and have triangular distribution. But limitations of supply capacity in suppliers and thermal capacity in lines are presented as deterministic (crisp) value. Thus in fuzzy notation, these constraints are expressed as follows:
(21) |
Equation 21 doesn’t have a simple true or false value. For measuring the possibility of occurrence Eq. 21, we have to define a Exposure Risk (EX) which means the minimum degree of α-cut that all values of this cut are less than xmax for ![]() or more than xmin for
or more than xmin for ![]() The final exposure risk for every solution (vector) k of the problem is calculated as shown in Fig. 4 and 5:
The final exposure risk for every solution (vector) k of the problem is calculated as shown in Fig. 4 and 5:
 | |
| Fig. 4: | The maximization constraint of |
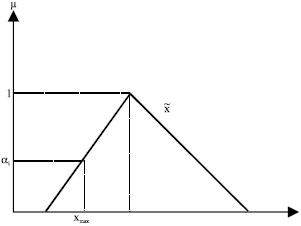 | |
| Fig. 5: | The minimization constraint of |
 | (22) |
Solution analysis: By modeling loads as fuzzy numbers and using fuzzy arithmetic (Lai and Hwang, 1992), the GENCOs payoffs are fuzzy numbers, but not TFNs, as:
(23) |
Applying fuzzy game theory concepts (Wu and Soo, 1999), the optimal bidding strategies can be obtained through three following steps.
Step 1: Using the removal function with several distinct cuts (distributed between 0 and 1) and based on the linearity property of removal function, the set of non-dominated strategies in Nash points for each GENCO is obtained. In the other words, the removal function transforms the fuzzy payoff function to a crisp value. Then the optimal strategy for each GENCO is calculated in the same way as the deterministic case.
After analyzing the set of non-dominated solutions, the GENCO can select the final non-dominated solution, considering the most satisfactory strategy according to its experience and professional point of view or uses the following steps to determine it.
Step 2: Each solution k in the set of non-dominated solutions has an associated vector of values ![]() that can be normalized as:
that can be normalized as:
(24) |
where, ![]() and EXmax are the removal values of the maximum values obtained for the GENCOs payoffs functions and for the exposure function, respectively and
and EXmax are the removal values of the maximum values obtained for the GENCOs payoffs functions and for the exposure function, respectively and ![]() and EXmin are the removal values of the minimum values obtained. Note that the result of this normalization gives the vector (1,...,1,1) for the ideal point (
and EXmin are the removal values of the minimum values obtained. Note that the result of this normalization gives the vector (1,...,1,1) for the ideal point (![]() ∀I ε G, EXmin) and the vector (0,...,0,0) for the anti-ideal point (
∀I ε G, EXmin) and the vector (0,...,0,0) for the anti-ideal point (![]() ∀I ε G, EXmax), that is, it represents the level of satisfaction for each GENCO.
∀I ε G, EXmax), that is, it represents the level of satisfaction for each GENCO.
Step 3: A max-min approach (Lai and Hwang, 1992), shown in Eq. 25, is applied to select the best (final) solution (that is, the most satisfactory solution using the aforementioned approach):
(25) |
Probabilistic model: Here, it is assumed that the power demand at each bus is normally distributed ![]()
Among various stochastic models, the chance-constrained programming, applied by Chouchman et al. (2005), is utilized and can be defined as:
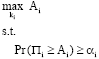 | (26) |
where, Pr{Πi≥Ai} is the probability degree. The constraint shows that in αi x 100% of the simulations, the profit of GENCO I is above Ai and the value of αi is specified by GENCO I.
If Πi(Qd, ki) is nondecreasing in Qd and ![]() then the ki is obtained as (Chouchman et al., 2005):
then the ki is obtained as (Chouchman et al., 2005):
(27) |
where, Φ(ri) = αi and Φ is the normal tail distribution function: Pr (Z≥z) = Φ (z) for Z~N(0,1).
The profit functions of GENCOs in Eq. 14 would be a second-order equation and are nondecreasing in Qd, if and only if the two following conditions are satisfied.
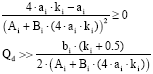 | (28) |
These two conditions will be met in most cases, so we have the deterministic optimization problem (Eq. 16) in which the random variable Qd is replaced by ![]()
NUMERICAL RESULTS
The two approaches for modeling the load forecast uncertainty will be compared by applying them to a network in which nine GENCOs compete. It’s assumed that all transmission lines have large enough capacity. The GENCOs’ cost functions data is given in Table 1. Also, in the case of fuzzy approach, the fuzzy demand is equal to ![]() and in the case of stochastic approach, the random demand is equal to
and in the case of stochastic approach, the random demand is equal to ![]() The optimal bidding strategies of GENCOs in these two cases are presented in the following sections, respectively.
The optimal bidding strategies of GENCOs in these two cases are presented in the following sections, respectively.
Fuzzy approach: The three steps mentioned above. Sections are applied to compute strategies and profits of all GENCOs.
Step 1: For various Bender cuts from 0 to 1, GENCOs’ profits and exposure risks is computed using removal function. Figure 6 and 7 show the profit and the exposure risk of GENCO 7 for different Bender cuts from 0 to 1. For other GENCOs, the profits have an upward trend in terms of Bender cut magnitude, like GENCO 7 and are not shown here for brevity.
| Table 1: | GENCOs cost function data |
 | |
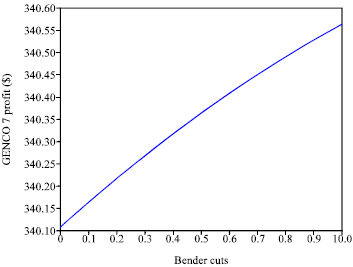 | |
| Fig. 6: | The variation of GENCO 7 profit |
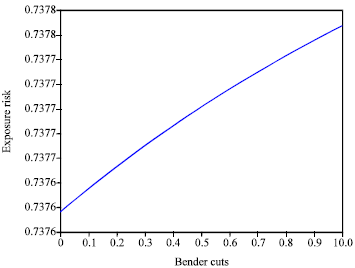 | |
| Fig. 7: | The variation of exposure risk for GENCO 7 |
Step 2 and 3: After normalizing profits and exposure risks of the nine GENCOs and drawing them in a same figure in terms of the corresponding Bender cuts, the final (best) solution, as shown in Fig. 8, can be found via a max-min operator.
In Fig. 8, the upward curves are GENCOs profits variations and the downward curves are exposure risk variations in terms of different Bender cuts from 0 to 1. Closeness of the profit variations of GENCOs and exposure risk variation causes that their normalized removal functions have matching plots as shown in Fig. 8.
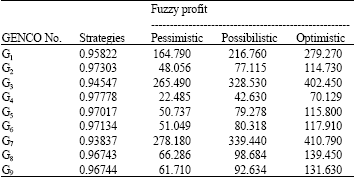
The GENCOs strategies and the pessimistic, possibilistic and optimistic values of the fuzzy profits of GENCOs in the best point calculated in Fig. 8, are shown in Table 2.
In this solution, the main part of GENCO 7 production fuzzy value is out of the maximum capacity as shown in Fig. 9.
 | |
| Fig. 8: | Normalized removal function of GENCOs’ profits |
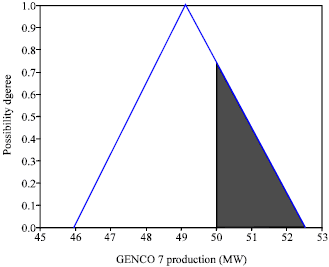 | |
| Fig. 9: | The TFN of GENCO 7 production |
| Table 2: | GENCOs strategies and profits values |
 | |
To reduce the exposure risk, it is possible to set the production of GENCO 7 to its maximum and repeat the three steps to find a better solution.
Here, the calculated exposure risk would be equal to zero. The best solution is determined in the same way as the earlier condition shown in Fig. 10.
In Fig. 10, the downward curve shows the profit of GENCO 7 and the upward curves show other GENCOs’ profits in terms of different Bender cuts from 0 to 1.
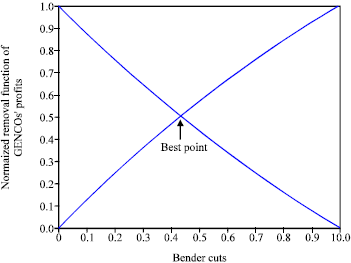 | |
| Fig. 10: | Normalized removal function of GENCOs’ profits |
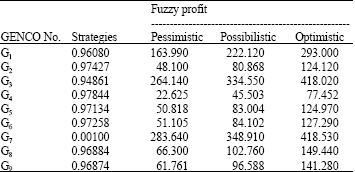
| Table 3: | GENCOs strategies and profits values |
 | |
It is necessary to note that the closeness of the profit variations of GENCOs and exposure risk variation causes the similarity of Fig. 8 and 10 and is not a general rule for all networks.
The GENCOs strategies and the pessimistic, possibilistic and optimistic values of the fuzzy profits of GENCOs of the best point calculated in Fig. 10 are shown in Table 3. The strategy of GENCO 7 doesn’t have any effect on the results obtained for other GENCOs. In addition, Table 3 shows that the GENCOs’ profits in imperfect competition in which the GENCO 7 reaches to its maximum capacity are more than perfect competition, as given in Table 2, in which there aren’t any limitations on the GENCOs productions and the thermal capacity of network lines.
Probabilistic approach: Here, it was detailed how the ordinal deterministic optimization is used to solve this stochastic optimization. Table 4 gives the strategy and the threshold profit of each GENCO at the Nash point when all players are using probabilities of 0.9 and 0.7 in their CCPs. Also, GENCO 7 produces its maximum capacity.
| Table 4: | GENCOs strategies and profits value |
 | |
Comparison: These two approaches for modeling the load forecast uncertainty calculate an optimal bidding strategy for each GENCO and the solutions of them are close to each other but aren’t exactly the same. In probabilistic approach, accurate estimation of the αi (or ri) values for each GENCO are needed which is not possible. In addition, normal distribution lacks the flexibility of fuzzy (possibility) distributions. Thus the result of probabilistic approach may be inferior to the optimal strategies obtained by fuzzy approach.
CONCLUSION
In a fully competitive electricity market, each participant should bid at its marginal cost in order to maximize its revenue. However, a practical electricity market, like Iranian market, is not a perfectly competitive one because of the particular characteristics such as the severe generation and transmission capacity limitations. So, it is critical for a GENCO to devise a good bidding strategy in order to maximize its potential profit.
It is proved in this study that the bilevel optimization problem, or equivalently, the MPEC program, are used for determining the optimal bidding strategies of GENCOs, can be converted to an ordinal one-level optimization problem. Furthermore, the NE is calculated by solving simultaneously this optimization problem for all GENCOs.
One of the usual uncertainties in this game-based problem is the uncertainty of load forecast. There are two approaches (fuzzy and probabilistic) for modeling this uncertainty in the literature. In this study, a fuzzy approach is developed for modeling the load forecast uncertainty and compared with the probabilistic one. Test results show that the fuzzy approach is more general than the probabilistic approach.
APPENDIX
Fu and Li (2006) has shown that the LMP components in a lossless DC network model include marginal energy and congestion cost as:
(29) |
where, λ and π are the dual variables from Eq.7 and SF is the shift factor which is the sensitivity of a line flow to a bus generation increment (injection) (Wood and Wollenberg, 1996).
Let us consider a transmission-unconstrained case (thus π = 0) and further assume that GENCOs in cap+ set are limited in their maximum capacity. So, the inequality constraint Eq. 5 is active for all GENCOs in cap set (that is the union of cap+ and cap– sets). Under these conditions the subproblem Eq. 2-6 is simplified to:
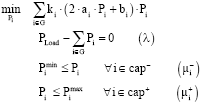 | (30) |
For calculating the dual variable, we have to setup the Lagrange equation for the problem as:
(31) |
Using the KKT conditions, the following expressions will be calculated:
(32) |
(33) |
(34) |
(35) |
Solving the Eq. 33-35 in terms of Pi and substituting in Eq. 32, yields the LMP expressions as:
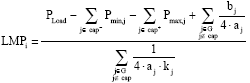 | (36) |
Moreover, with the assumption of bidding the transmission inequalities, the LMP expression can be calculated the same and are the form of Eq. 8 but in which the Ai, Bi and LDi parameters have different expressions.
NOTATION
The notations used in this study are as follows. For a dummy variable x, the notation xi for I = 1...n, is used to refer to each element of vector x. The lower and upper bound on the value of xi is represented by ![]() respectively. u ⊥ v is used to represent the relation uT . v = 0 . diag(ω) is used for the square matrix whose diagonal elements are the elements of ω and whose other elements are zero.
respectively. u ⊥ v is used to represent the relation uT . v = 0 . diag(ω) is used for the square matrix whose diagonal elements are the elements of ω and whose other elements are zero.
The electrical network is composed of N nodes with G GENCOs, indexed by I or j. A demand at node I is represented by QDi. Total demand of this network is represented by PLoad. The set of arcs is shown by A and if ij ε A there is an arc between I and j. The power flow between nodes I and j is represented by ![]() is the capacity limit of the line connecting nodes I and j. L is the set of Kirchhoff loops in the network, indexed by m such that Lm is the ordered set of arcs associated with Kirchhoff loop m . zij is the reactance on arc ij ε L and sijm = ±1, depending on the orientation of arc ij in loop m. R denotes the (arc, loop) incidence matrix which is equal to sijmzij if ij ε L and is zero otherwise. Δ denotes the (node, arc) incidence matrix of the electrical network whose entries Δil are + 1 if l = ij and -1 if l = ji and are zero otherwise (ij ε set of arcs and j ε set of network nodes).
is the capacity limit of the line connecting nodes I and j. L is the set of Kirchhoff loops in the network, indexed by m such that Lm is the ordered set of arcs associated with Kirchhoff loop m . zij is the reactance on arc ij ε L and sijm = ±1, depending on the orientation of arc ij in loop m. R denotes the (arc, loop) incidence matrix which is equal to sijmzij if ij ε L and is zero otherwise. Δ denotes the (node, arc) incidence matrix of the electrical network whose entries Δil are + 1 if l = ij and -1 if l = ji and are zero otherwise (ij ε set of arcs and j ε set of network nodes).
Cap+ and cap– are the sets of generating companies that should produce their maximum and minimum capacity, respectively. cap is the union of these two sets.
The marginal cost curve of every single supplier is assumed to be affine in the form MCi = 2.ai . Pi + bi, where, ai and bi are the coefficients of cost function that is in the form ![]() . For each player I in the game, ki and Πi(ki) denote its strategy and payoff, respectively and k–I denotes its rivals strategies.
. For each player I in the game, ki and Πi(ki) denote its strategy and payoff, respectively and k–I denotes its rivals strategies.
REFERENCES
- Amjady, N. and M. Hemmati, 2006. Energy price forecasting: Problems and proposals for such predictions. IEEE Power Energy Mag., 4: 20-29.
CrossRef - Arroyo, J.M. and A.J. Conejo, 2000. Optimal response of a thermal unit to an electricity spot market. IEEE Trans. Power Syst., 15: 1098-1104.
Direct Link - Baldick, R., 2002. Electricity market equilibrium models: The effects of parameterization. IEEE Trans. Power Syst., 17: 1170-1176.
CrossRef - Chouchman, P.B. Kouvaritakis, M. Cannon and F. Prashad, 2005. Gaming strategies for electric power with random demand. IEEE Trans. Power Syst., 20: 1283-1292.
CrossRef - David, A.K. and F. Wen, 2000. Strategic bidding in competitive electricity market: A literature survey. IEEE Power Eng. Soc. Summer Meeting, 2000: 2168-2173.
CrossRef - Guan, X., Y.C. Ho and F. Lai, 2001. An ordinal optimization based bidding strategy for electric power suppliers in the daily energy market. IEEE Trans. Power Syst., 16: 788-797.
Direct Link - Haghighat, H., H. Seifi and A.R. Kian, 2007. Gaming analysis in joint energy and spinning reserve markets. IEEE Trans. Power Syst., 22: 2074-2085.
CrossRef - Hobbs, B.F., C.B. Metzler and J.S. Pang, 2000. Strategic gaming analysis for electric power systems: An MPEC approach. IEEE Trans. Power Syst., 15: 638-645.
Direct Link - Li, T., M. Shahidehpour and Z. Li, 2002. Optimal response of a power generator to energy, AGC and reserve pool-based markets. IEEE Trans. Power Syst., 17: 404-410.
Direct Link - Li, T. and M. Shahidehpour, 2005. Strategic bidding of transmission-constrained gencos with incomplete information. IEEE Trans. Power Syst., 20: 437-447.
CrossRef - Li, T. and M. Shahidehpour, 2005. Price-based unit commitment: A case of lagrangian relaxation versus mixed integer programming. IEEE Trans. Power Syst., 20: 2015-2025.
CrossRefDirect Link - Li, T., M. Shahidehpour and Z. Li, 2007. Risk-constrained bidding strategy with stochastic unit commitment. IEEE Trans. Power Syst., 22: 449-458.
CrossRef - Popovic, D.S. and Z.N. Popovic, 2004. A risk management procedure for supply restoration in distribution networks. IEEE Trans. Power Syst., 19: 221-228.
CrossRef - Rosado, I.J.R. and J.A.D. Navarrov, 2004. Possibilistic model based on fuzzy sets for the multiobjective optimal planning of electric power distribution network. IEEE Trans. Power Syst., 19: 1801-1810.
CrossRef - Weber, J.D. and T.J. Overbye, 2002. An individual welfare maximization algorithm for electricity markets. IEEE Trans. Power Syst., 17: 590-596.
CrossRef








