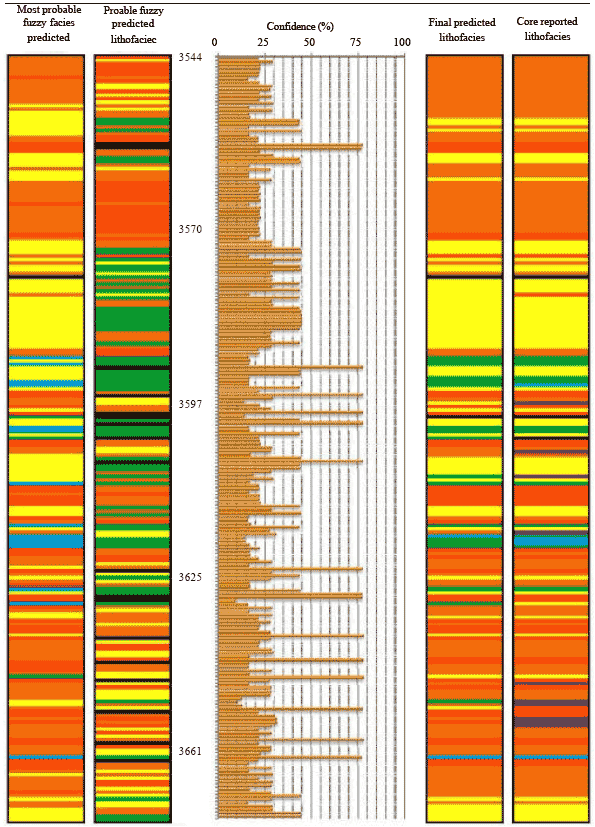
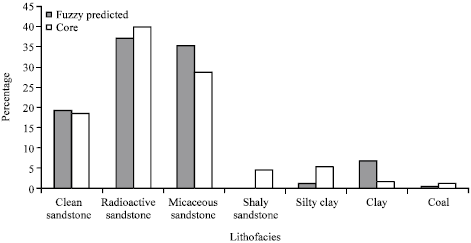
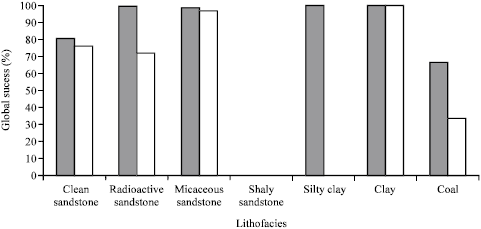
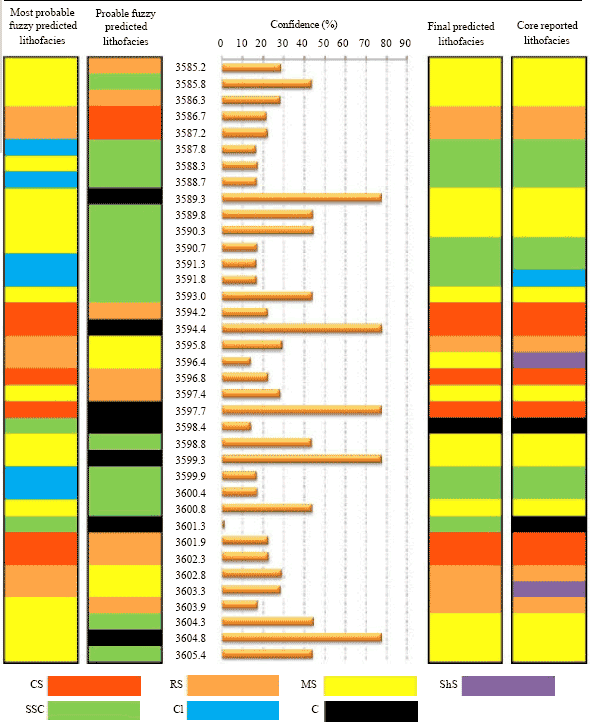
Research Article
New Approach of Fuzzy Logic Applied to Lithofacies Forecasting and Permeability Values Estimation
Reservoir Engineer, NIOC, Pars Oil and Gas Compoany, North Pars Branch, Parvin Street, Fatemi Blv., Tehran, Iran
B. Movahed
Department of Petrophysic, NIOC, Pars Oil and Gas Company, Parvin Street, Fatemi Blv., Tehran, Iran