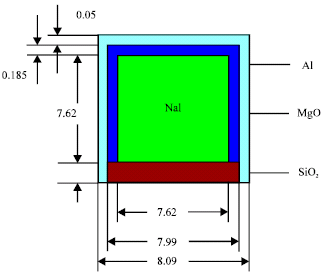
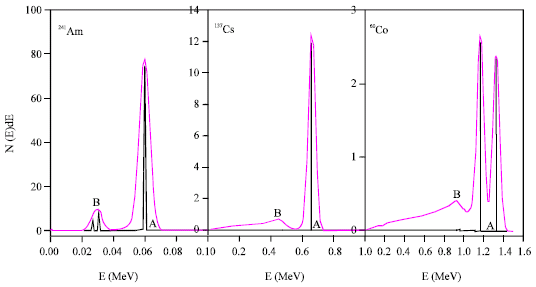
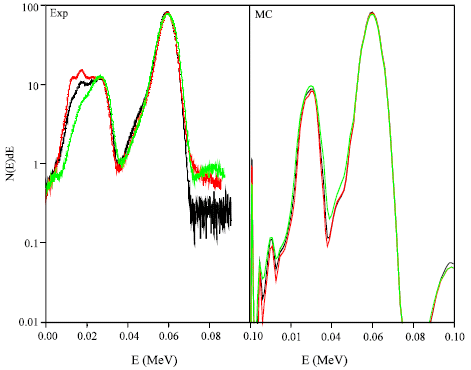
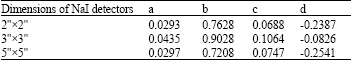Research Article
The Effect of Detector Dimensions on the NaI (Tl) Detector Response Function
Department of Physics, Faculty of Physics, Shahrood University of Technology, Shahrood, Iran
R. Izadi-Najafabadi
Department of Physics, Faculty of Sciences, Ferdowsi University of Mashhad, Mashhad, Iran
H. Miri-Hakimabad
Department of Physics, Faculty of Sciences, Ferdowsi University of Mashhad, Mashhad, Iran