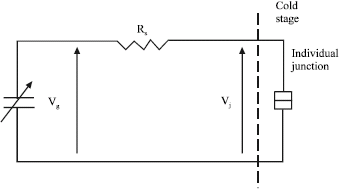
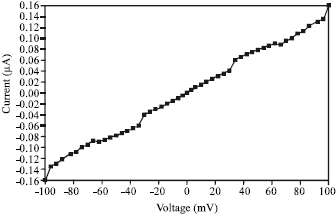
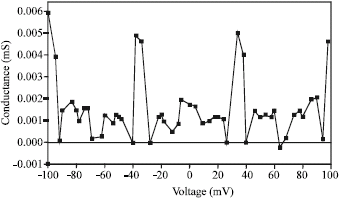
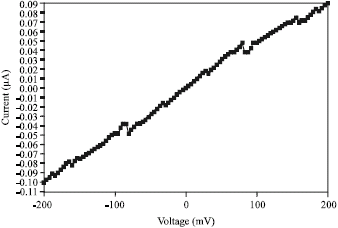
Research Article
Electrical Investigations of YBa2Cu3O(7-x) (0 ≤ x ≤ 0.5) Tunnel Junctions
Laboratory of Semiconductors, Department of Physics, University Badji Mokhtar, Annaba, Algeria
B. Hadjoudja
Laboratory of Semiconductors, Department of Physics, University Badji Mokhtar, Annaba, Algeria