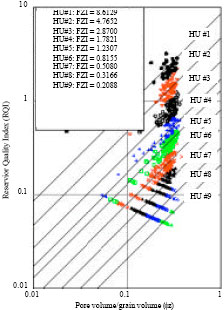
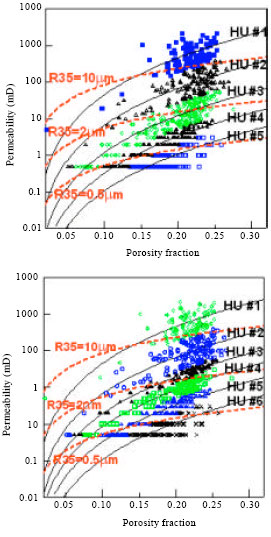
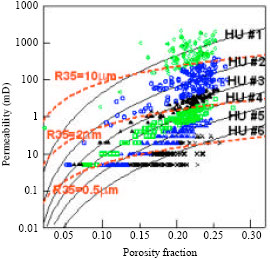
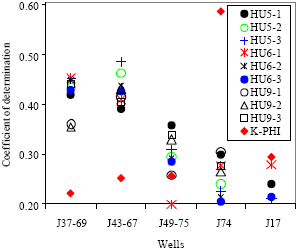
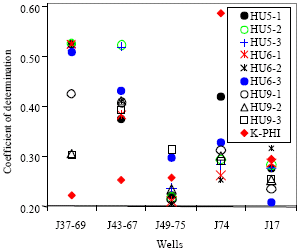
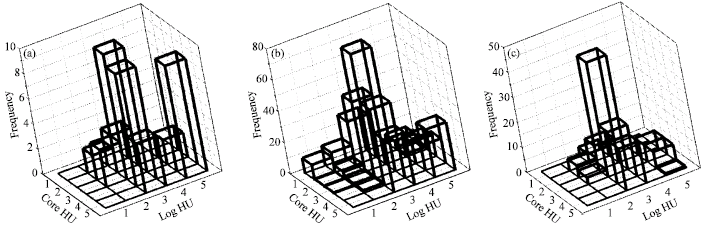
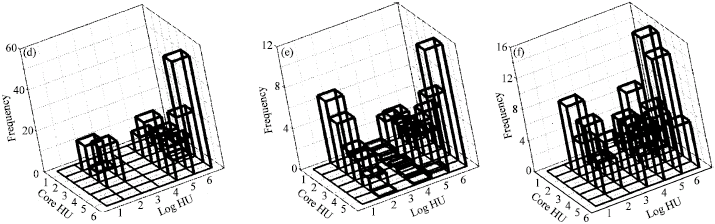
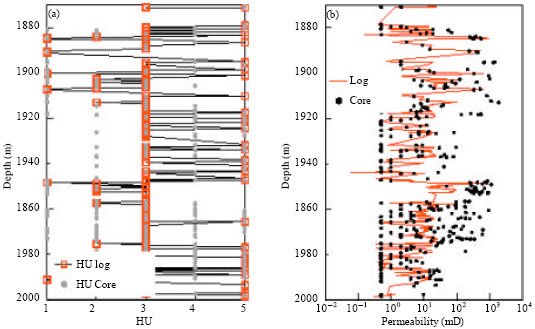
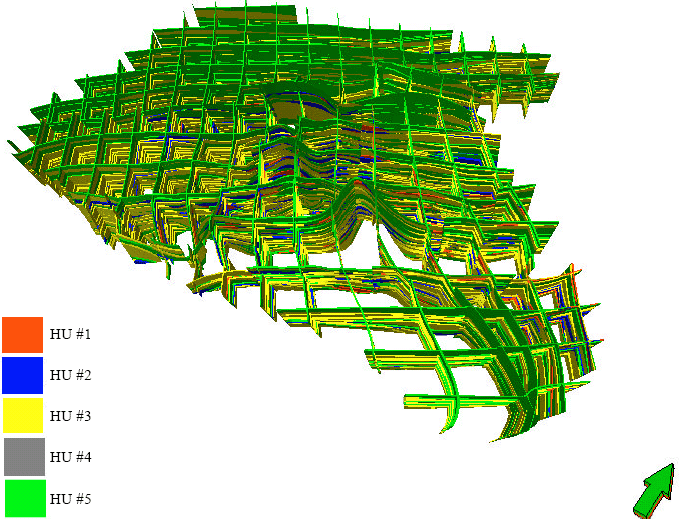
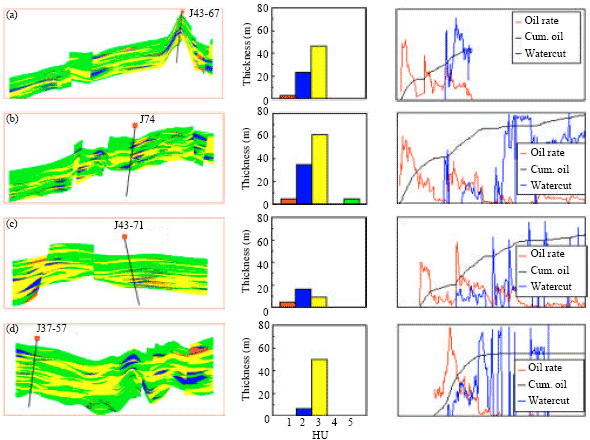
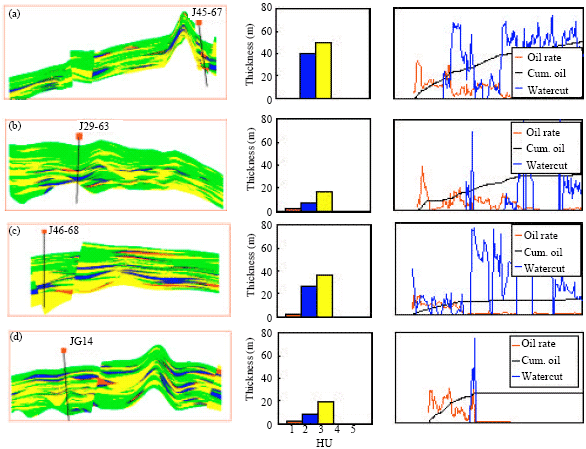
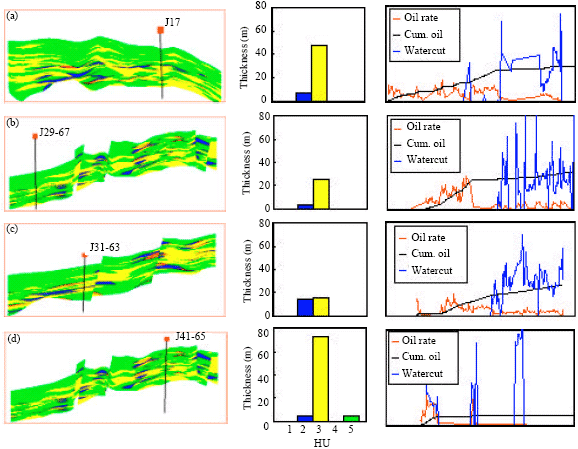
Case Study
Hydraulic (Flow) Unit Determination and Permeability Prediction: A Case Study of Block Shen-95, Liaohe Oilfield, North-East China
Faculty of Resources, China University of Geosciences (Wuhan), Wuhan 430074, People Republic of China
Z. Tang
Faculty of Environmental Studies, China University of Geosciences (Wuhan), Wuhan 430074, People Republic of China
Q. Fei
Faculty of Resources, China University of Geosciences (Wuhan), Wuhan 430074, People Republic of China