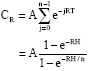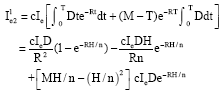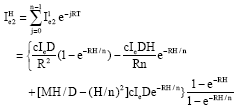Research Article
A Cash Flow Oriented EOQ Model with Deteriorating Items Under Permissible Delay in Payments
Department of Business Administration, Graduate School of Management, The Overseas Chinese Institute of Technology, Taichung, Taiwan, Republic of China
Li-Chiao Lin
Department of Business Administration, National Chinyi University of Technology, Taichung County, Taiwan, Republic of China