Case Study
Forecasting Precipitation with Artificial Neural Networks (Case Study: Tehran)
Department of Physical Geography, University of Kurdistan, Iran
M. Darand
Departmant of Physical Geography, University of Isfahan, Iran
The ANN modeling framework has been used increasingly in various aspects of science and engineering because of its ability to model both linear and nonlinear systems without the need to make any assumptions as are implicit in most traditional statistical approaches.
It has been shown by Hornik et al. (1989) that an ANN with sufficient complexity is capable of approximating any smooth function to any desired degree of accuracy.
Some of the hydrologic problems ANN has been used for include rainfall-runoff modelling (Hsu et al., 1995; Smith and Eli, 1995; Achela et al., 1998), scheduling of hydroelectric power systems (Saad and Bigras, 1996) and river flow prediction (Karunanithi et al., 1994; Zhu and Fujita, 1994). The ANN methodology has been applied also to forecast rainfall; for example, French et al. (1992) used synthetically generated rainfall storms to calibrate an ANN model and then generated plausible rainfall sequences that could occur over a catchments using a physically based rainfall to validate the ANN. The main advantage of ANN is in cases where intrinsic nonlinearities in the dynamics prevent the development of exactly solvable models. Note that, in meteorology, all of these criteria are present in the sense that the dynamics are inherently nonlinear and prediction is one of the main goals. ANN has been used successfully to model rainfall in meteorological applications (Navonne and Ceccatto, 1994). Xiao and Chandrasekar (1997) have developed a three-layer perceptron ANN based algorithm for rainfall estimation from reflectivity of radar observations. The objective of this investigation is forecasting precipitation with artificial neural networks.
The artificial neural networks approach: An ANN is composed of an input layer of neurons, one or more hidden layers and an output layer. Each layer comprises multiple units connected completely with the next layer (Fig. 1), with an independent weight attached to each connection. The number of nodes in the output layer is equal to the number of values to be predicted.
 | |
| Fig. 1: | Network model for precipitation forecasting |
Back propagation algorithm: One of extensively used ANN models for system modeling application is the multilayer perceptron model based on the BP (Erb, 1993). Multilayer perceptrons (MLPs) are layered feed forward networks typically trained with static back propagation. These networks have found their way into countless applications requiring static pattern classification. Their main advantage is that they are easy to use and that they can approximate any input/output map. The key disadvantages are that they train slowly and require lots of training data (typically three times more training samples than network weights). In the BP algorithm learning based, the initial weights of connections are randomly chosen. Suppose we have N learning examples with each example having n inputs and l outputs, the input vector can be described as Xj = (X1j, …, Xnj) and the output vector as Aj = (B1j , …, Blj), 1 ≤ j ≤ N. The learning process takes place using the following two steps.
Forward propagation: The input vector Xj is fed into the input layer and an output vector Oj = (O1j, …, Olj) is generated on the basis of the current weights W = (W1l,..., Wnl). The value of Bj is compared with the actual output Aj and the output differences are summed to generate an error function E defined as:
(1) |
Error back propagation: In this step, the error from Eq. 1 is back propagated by performing weights update using gradient descent as follows:
(2) |
where, 0 < η < 1 is a parameter controlling the convergence rate of the algorithm. The process of forward propagation and error back propagation continues until E converges to a predefined small value. ΔWnl is accumulated and updated after a complete run of all the N examples for our research.
The basic BP algorithm described above is often very slow to converge in real practice. In order to overcome the obstacles of these problems, BP algorithm has adopted many improvement techniques. Initializing the BP weights with GA contains many merits hence attracts the scholars and researchers interesting (Sexton et al., 1998). And its modern form is derived mainly from Holland’s study in the 1960s.
 | |
| Fig. 2: | Flowchart of micro algorithm genetic |
As has been shown in Fig. 2, GA is capable of solving wide range of complex optimization problems only using three simple genetic operations (selection, crossover and mutation) on coded solutions (strings, chromosomes) for the parameter set, not the parameters themselves in an iterative fashion. GA considers several points in the search space simultaneously, which reduces the chance of convergence to a local optimum. At first a random population is generated. This population feeds the population memory, which is divided in two parts. The non-replaceable portion of the population memory will never change during the entire run and is meant to provide the required diversity for the algorithm. The initial population of the micro-GA at the beginning of each of its cycles is taken (with a certain probability) from both portions of the population memory as to allow a greater diversity. During each cycle, the micro-GA undergoes conventional genetic operation: tournament selection, two-point crossover, uniform mutation and elitism (only one nondominated vector is arbitrarily selected at each generation and copied intact to the following one). After the micro-GA finishes one cycle (i.e., when nominal convergence is achieved), two nondominated will chose vectors from the final population (the first and last) and compare them with the contents of the external memory (this memory is initially empty). If either of them (or both) remains as nondominated after comparing against the vectors in this external memory, then they are included there. All the dominated vectors are eliminated from the external memory. These two vectors are also compared against two elements from the replaceable portion of the population memory (this is done with a loop, so that each vector is only compared against a single position of the population memory). If either of these vectors dominates to its match in the population memory, then it replaces it. The idea is that, over time, the replaceable part of the population memory will tend to have more nondominated vectors. Some of them will be used in the initial population of the micro-GA to start new evolutionary cycles (Carlos et al., 2001).
Study area: The city of Tehran, the capital city of Iran, is located in Tehran Province. This city having more than 7 million people is the most populated city in the country. The city is surrounded by Alborz Mountains in the Northeast. Figure 3 shows the geographic location of study area.
Data used: In this study, monthly precipitation data obtained from Tehran Meteorology Center for Tehran station from 1950 to 2003.
Method: The samples were divided into two sets. The first set is the learning set for the ANN training, while the other set represents the holdout set for pollution prediction to verify the efficiency and correctness of the cutting force model. With these collected data, the ANN system is ready to launch its training scheme. TanhAxon function that is a most important function in B.P method is used as irritates function. Neural solutions software is used for training artificial network. To reduce forecasting error, train and error on the network parameters carried out and at the end parameters arranged as has been shown in Table 1.
| Table 1: | Network parameters are trained after train and error |
 | |
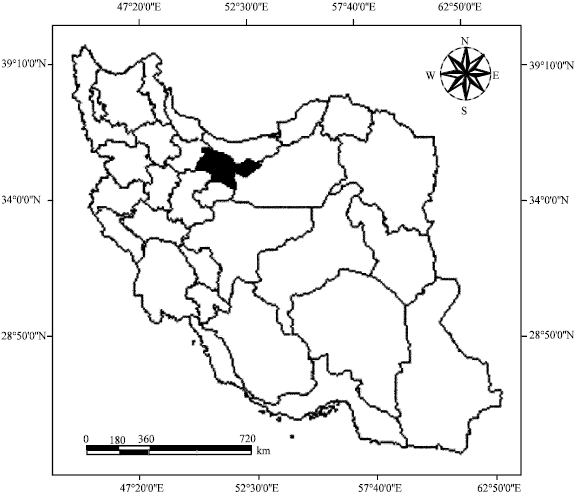 | |
| Fig. 3: | The geographic location of study area that highlighted with black color |
Momentum is one of the main parameters in training that show the fraction of before weights effect to new weights. Neuron is smallest processing unit of hidden layer and learning coefficient control the speed of collation the weights among neurons.
RESULTS AND DISCUSSION
The objective of this investigation was forecasting precipitation with artificial neural networks. To achieve this objective two models in accordance with the methods of determining the connection weights of BP and hybrid of GA-BP are compared with the real experimental results. The results of trained network without GA showed in Fig. 4.
There is a good coordination between real data (precipitation) with ANN forecast. There is a nonlinear correlation between monthly precipitation that is one of the reasons of increase artificial networks accuracy rather than classic models such as regression models that are linear.
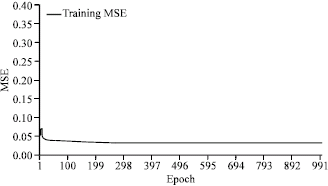
Figure 5 shows minimum training error of network without combined with GA. Minimum training error of network after training equal to 0/04.
Correlation coefficient presents relation rate between network outputs with real data (precipitation).
 | |
| Fig. 4: | Comparing amount of real precipitation data with ANN forecast |
 | |
| Fig. 5: | Minimum training error of network with ANN |
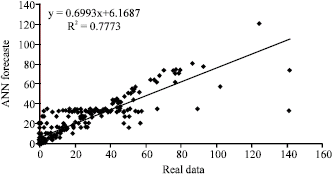
Correlation coefficient equal to 1, shows fulfill coordination between real data (precipitation) with ANN forecast and -1 show no coordination between them. Figure 6 shows correlation and adjust coefficient between real data (precipitation) with ANN forecast that equal to 0/77.
As described above the basic BP algorithm is often very slow to converge in real practice. In order to overcome the obstacles of these problems, the BP weights with GA was used. The result of this combination showed in Fig. 7. Figure 8 shows the minimum training error of network. Minimum training error of network rate after training approximately equal to 0/03.
 | |
| Fig. 6: | Correlation between real precipitation data with ANN forecast |
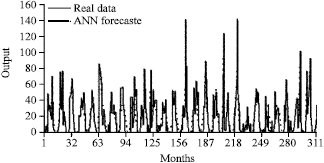 | |
| Fig. 7: | Comparing amount of real precipitation data with ANN-GA forecast |
 | |
| Fig. 8: | Minimum training error of network in combination with ANN-GA |
 | |
| Fig. 9: | Correlation between real precipitation data in combination with ANN-GA forecast |
Figure 9 showed Correlation between real data (precipitation) with combination ANN-GA forecast. The adjust coefficient equal to 0/83.
Classic or liner models are used for trends that with increase a parameter another parameter increases or decreases. Thus using of these models for nonlinear trends increase mistake rate. The neural networks can be a useful tool to model the relation between variables because we can consider the ANNs as being very general forms of non-linear regression models. In fact, they can model time series very effectively (Chakraborty et al., 1992) and are employed when the classic methods do not work. There is a nonlinear trend for precipitation. For forecasting this nonlinear trend must use nonlinear models. One of these nonlinear models is artificial neural networks forecasting model. The results after testing network with hidden layers and different learning coefficients showed that using artificial neural networks with one perceptron with 1 hidden layers, 0/1 learning coefficient and 0/7 momentum result in a relative better model and after retraining and testing network with different hidden layers and learning coefficients in combination with Genetic algorithm cause decrease error and increase the speed of calculations and present a better model.
| • | Artificial networks forecast the nonlinear trend of monthly precipitation |
| • | The combinations of algorithm genetic with artificial network increase the speed of analyzing and processing accuracy. In other hand decrease error rate |
The authors appreciate Professor Seyyed Abolfazl Massodian (Department of Climatology, Isfahan University, Iran) for reviewing the manuscript and for his useful comments.